朱信忠(核能研究所)
摘要
Kolmogorov-Smirnov 統計測試法(簡稱KS-test)被廣泛地應用來分析分佈型之數據組,KS-test不需對樣本數據組之分佈做任何假設,它對樣本數據組之CDF曲線的形狀及位置敏感,只在乎數據組間的相對分佈,而與X-軸的座標尺規無關。
本文介紹KS-test的理論背景與進行KS-test所需之數學式,並詳細地說明其應用的方法與步驟。本文也提出一套蒙地卡羅測試方法與執行步驟,以(0~1)之均一分佈函數及標準化常態分佈函數,來驗證目前被廣泛使用之Kolmogorov分佈修正函數。
本文特根據所介紹之數學式及方法與步驟,以微軟Visual Basic程式語言將之撰寫成一套在微軟Windows環境下操作之電腦程式,並應用此自撰之電腦程式於兩個範例的分析展示。
關鍵字:Kolmogorov-Smirnov、統計測試、數據分析
壹、前言
Kolmogorov-Smirnov 統計測試法(簡稱KS-test)是一種統計學上的數據分析技術,它專門針對分佈型數據組(distributed data set)進行測試,而非針對單一的離散數據(single discrete data)(Young, 1977;Fasano and Franceschini, 1987;Justal et al., 1997;Chen and Hong, 1997;Kar and Mohanty, 2006;Meintanis, 2007)。KS-test被廣泛地應用來測試某一分佈型數據組是否出自某一參考分佈函數如均一分佈(uniform distribution)、常態分佈(normal distribution或稱Gaussian distribution)、指數分佈(exponential distribution)等等,對於這種情況下的測試,學術界上稱它為一組樣本測試(one-sample test,簡稱OST);KS-test 也被廣泛地應用來測試某兩分佈型數據組是否出自同一分佈函數,對於這種情況下的測試,學術界上稱它為兩組樣本測試(two-sample test,簡稱TST)。KS-test具有下列數項優點:
l 不需對樣本數據組之分佈做任何假設,以學術術語來說,它是一種non-parametric及distribution free的測試技術。以Student’s t-test為例,Student’s t-test假定受測數據組呈常態分佈,而且各數據組間的差別主要在平均期望值,若應用Student’s t-test於非常態分佈數據組的測試,將可能增大測試錯誤的風險;另外x2 test(讀成Chi squared test)則假定取樣誤差呈Gaussian分佈;
l 使用數據組之累積密度函數(cumulative density function,簡稱CDF)曲線來進行測試,對CDF曲線之形狀及位置敏感,只在乎數據組間的相對分佈,與所使用之X-軸的座標尺規(scale)無關,因此可依最佳視覺效果而隨意採用線性(linear)尺規或對數(logarithmic)尺規;
l 將數據組以圖形方式顯示,令使用測試人員可以目視偵測數據組是否呈常態型分佈,以便更換適當的測試技術如Student’s t-test來進行測試;
l 穩定(robustness)。
本文將大略地介紹KS-test的理論背景與進行KS-test所需之數學式,詳細地說明應用的方法與步驟,並進行一些範例展示。本文也提出一套蒙地卡羅(Monte Carlo)測試方法與執行步驟,以(0~1)之均一分佈函數(uniform distribution)及標準化常態分佈函數(standardized normal distribution),來驗證目前被廣泛使用之Kolmogorov分佈修正函數。為了展示KS-test的應用與結果,本文特根據文中所介紹之數學式及方法與步驟,以微軟Visual Basic程式語言,將之撰寫成一套在微軟Windows環境下操作之電腦程式,並應用此自撰之電腦程式於兩個範例之分析展示。
貳、理論背景
2.1 KS-test之統計D值
KS-test之統計D值定義為(Drew et al., 2000):
對於一組樣本測試(OST)時,以符號Dn表示:
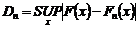 (1)
(1)
其中,F(x)為某一參考分佈函數之理論上的(theoretical)CDF曲線,其曲線形狀屬連續式,相當於數據點數無限多的情況;而Fn(x)為取樣數據組之CDF曲線,其曲線形狀屬階梯式,相鄰兩點間之機率差值為1/n,n為該取樣數據組之取樣數目(sample size),數據點數有限。
對於兩組樣本測試(TST)時,以符號Dm,n表示:
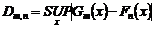 (2)
(2)
其中,Gm(x)與Fn(x)分別為該兩組取樣數據組之CDF曲線,其曲線形狀皆屬階梯式,Fn(x)曲線相鄰兩點間之機率差值為1/n,n為Fn(x)之取樣數目;而Gm(x)曲線相鄰兩點間之機率差值為1/m,m為Gm(x)之取樣數目,m與n都是有限的數據點數。
式(1)或式(2)中之SUP讀成supremum,其數學上之意義為:尋找兩道分佈曲線間之最大垂直差距。因此,Dn或Dm,n就是兩道CDF曲線間之最大垂直差距絕對數值。在數學式的表示上,文獻中有時也常以MAX取代SUP,對於現代的讀者較易瞭解(Young, 1977)。由於機率之最小數值為0.0(F(-∞)=0.0)、最大數值為1.0(F(∞)=1.0),故Dn或Dm,n其數值一定皆會座落在0.0至1.0之間。以圖例來表示,則式(2)之結果如圖1所示,圖中之垂直紅線所示者即是Dm,n值(為方便起見圖中簡單以符號D來表示),其數值為0.45。另外,為了CDF曲線之視覺效果,圖1之橫座標也以對數尺規來表示;若橫座標以0~100之線性尺規來表示的話,則兩道CDF曲線重要之部分會擠在縱座標附近,視覺效果上顯得頗不美觀。

圖1 KS-test統計D值範例
2.2 Kolmogorov分佈函數
KS-test必須應用到Kolmogorov分佈函數,Kolmogorov於1933年推導出Kolmogorov分佈函數之漸近限值,其數學式為(Andrade et al., 2001;Greenwell et al., 2004;Wikipedia, 2009):
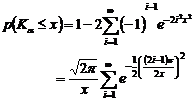 (3)
(3)
式(3)等號左邊之p(Kα≤x)為Kα≤x之機率(probability),可以寫為:
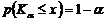 (4)
(4)
其中,α為重要度(significance level),而(1-α)則稱為信心度(confidence level)。
當nà∞時,Kolmogorov theorem (Wikipedia, 2009)證明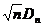 會趨近於Kolmogorov分佈(Kα),而且與F(x)的分佈型態無關:
會趨近於Kolmogorov分佈(Kα),而且與F(x)的分佈型態無關:
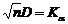 (5)
(5)
當實際進行數值分析時,通常m與n都不會太大,在此情況下,學術界慣用的修正公式為(Andrede et al., 2001;Greenwell et al., 2004):
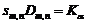 (6)
(6)
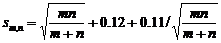 (7)
(7)
式(6)及式(7)是屬於兩組樣本測試(TST)的應用,當應用於一組樣本測試(OST)時,可令m值趨於∞,則式(6)及式(7)可以簡化而得:
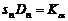 (8)
(8)
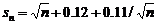 (9)
(9)
式(6)至式(9)稱為Kolmogorov分佈修正函數,配合式(3)及式(4)來使用。當n >> 100時,從式(9)可以看得出來 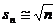 ,因此式(8)就等於式(5)。Kolmogorov 分佈函數(式(3)及式(4))之結果如圖2所示,圖中橫座標為α值,縱座標為Kα值。圖中之結果顯示:當α值在0~0.2之間時,Kα值隨α值之增加而急劇銳減;當α值在0.2~0.9之間時,Kα值隨α值之增加而緩慢減小;當α值大於0.9以後,Kα值隨α值之增加又快速減小。比較常應用之α值為0.05、0.01、或0.001,相當於信心度分別為95%、99%、及99.9%,Kα對應於α之部分重要關鍵數值則列於表1中。
,因此式(8)就等於式(5)。Kolmogorov 分佈函數(式(3)及式(4))之結果如圖2所示,圖中橫座標為α值,縱座標為Kα值。圖中之結果顯示:當α值在0~0.2之間時,Kα值隨α值之增加而急劇銳減;當α值在0.2~0.9之間時,Kα值隨α值之增加而緩慢減小;當α值大於0.9以後,Kα值隨α值之增加又快速減小。比較常應用之α值為0.05、0.01、或0.001,相當於信心度分別為95%、99%、及99.9%,Kα對應於α之部分重要關鍵數值則列於表1中。
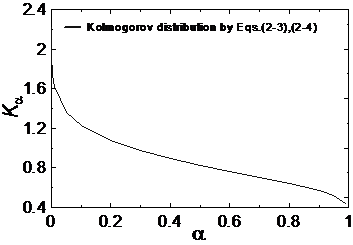
圖2 Kolmogorov分佈函數曲線
表1 Kα vs. α 之部分重要關鍵數值
|
α
|
Kα
|
α
|
Kα
|
α
|
Kα
|
|
0.99
|
0.4409
|
0.5
|
0.8275
|
1E-2
|
1.6276
|
|
0.95
|
0.5195
|
0.4
|
0.8947
|
5E-3
|
1.7308
|
|
0.9
|
0.5711
|
0.3
|
0.973
|
1E-3
|
1.9494
|
|
0.8
|
0.6447
|
0.2
|
1.0727
|
5E-4
|
2.0365
|
|
0.7
|
0.7067
|
0.1
|
1.2238
|
1E-4
|
2.2253
|
|
0.6
|
0.7661
|
5E-2
|
1.3581
|
---
|
---
|
2.3 Kolmogorov分佈修正函數之數值法驗證
在本節中將設計一套蒙地卡羅(Monte Carlo)的數值運跑法,來驗證 Kolmogorov 分佈函數(式(3)及式(4))在樣本數目不大時,與其目前被廣泛使用之修正函數(即式(8)及式(9))之曲線匹配(fitting)的情況,本驗證屬一組樣本測試(OST)。在本驗證中,所使用之參考分佈函數分別為:(0~1)之均一分佈函數及標準化常態分佈函數。(0~1)均一分佈函數其最小數值為0.0、最大數值為1.0,而標準化常態分佈函數之特性為:平均值為0.0、標準差(standard deviation)為1.0,在(-1.0~1.0)的範圍內涵蓋了68%的數值,在(-2.0~2.0)的範圍內涵蓋了95.5%的數值,在(-3.0~3.0)的範圍內涵蓋了99.7%的數值,在(-3.29~3.29)的範圍內則涵蓋了99.9%的數值。在本驗證中,將進行三種不同取樣數目的測試,取樣數目分別為n=10、n=50、及n=100等,在每一種取樣數目下,都將以蒙地卡羅法反復隨機取樣運跑100,000次後,再計算100,000個snDn值之分佈,並與Kolmogorov分佈函數(式(3)與式(4))進行分佈曲線匹配比較。當然,樣本數目越大則電腦運跑時間也就越長,但在本驗證範例中,當n=100時,以目前主流個人電腦來運跑,其運跑100,000次的耗時並沒有很長。本驗證之蒙地卡羅測試法的步驟如下:
1. 從參考分佈函數中隨機取出 n個離散數值樣本;
2. 將此n個離散數值樣本從小到大依序排列,做出一道此樣本之CDF分佈曲線(Fn(x));
3. 求取此樣本之CDF分佈曲線(Fn(x))與參考分佈函數CDF分佈曲線(F(x))間之最大垂直差距數值(即Dn)及snDn值,並加以儲存;
4. 反復1~3之步驟,直到共運跑100,000次為止;
5. 接著將上述之100,000個snDn值從小到大依序排列,得一道snDn之CDF分佈曲線,最小者(即第1個)之機率為1.0-5,最大者(即第100,000個)之機率為1.0,而且任意相鄰兩個snDn數據間之機率差值為1.0-5;
6. 將本snDn之CDF分佈曲線與Kolmogorov分佈函數(式(3)與式(4))進行比較。
本驗證之結果示於圖3及圖4中,圖3為測試均一分佈之結果,而圖4則為測試標準化常態分佈之結果。從圖3及圖4之結果可以很肯定地說:式(8)及式(9)是完全正確的。
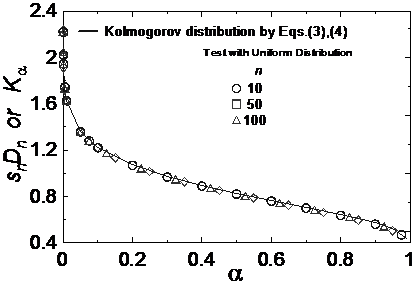
圖3 Kolmogorov分佈修正函數驗證(均一分佈)
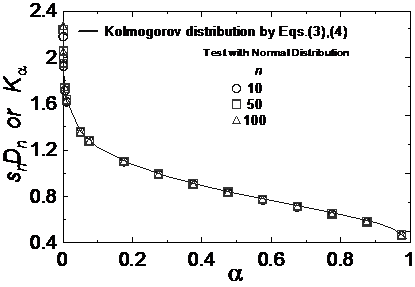
圖4 Kolmogorov分佈修正函數驗證(常態分佈)
參、應用方法與執行步驟
使用KS-test進行分析時,其執行步驟與統計判斷方法為:
3.1 一組樣本測試(OST)時:
1. 先備妥參考分佈函數之CDF分佈曲線圖(稱為F(x))或CDF分佈數據表列;
2. 將欲被分析之n個樣本數據組從小到大依序排列,建構出樣本數據組之CDF分佈曲線(稱為Fn(x));
3. 求取F(x)與Fn(x)間之最大垂直差距的絕對值(稱為Dn);
4. 以式(9)計算出snDn數值;
5. 利用圖2或表1找出snDn>=Kα時之對應α值;
6. 下判斷說:在(1-α)的信心度下,吾人認為F(x)與Fn(x)是屬不同的分佈;也就是說Fn(x)並不是從F(x)衍生而出的。例如當α=0.05時,snDn剛剛好大於或等於Kα,則吾人可以說:在95%的信心度下,F(x)與Fn(x)是屬不同的分佈。
3.2 兩組樣本測試(TST)時:
1. 將欲被分析之第一組 m個樣本數據組從小到大依序排列,建構出第一組樣本數據組之CDF分佈曲線(稱為Gm(x));
2. 將欲被分析之第二組 n個樣本之數據組從小到大依序排列,建構出第二組樣本數據組之CDF分佈曲線(稱為Fn(x));
3. 求取Gm(x)與Fn(x)間之最大垂直差距的絕對值(稱為Dm,n);
4. 以式(7)計算sm,nDm,n數值;
5. 利用圖2或表1找出sm,nDm,n>=Kα時之對應α值;
6. 下判斷說:在(1-α)的信心度下,吾人認為Gm(x)與Fn(x)是屬不同的分佈;也就是說Gm(x)與Fn(x)並非出自同一分佈函數。例如當α=0.05時,sm,nDm,n剛好大於或等於Kα,則吾人可以說:在95%的信心度下,Gm(x)與Fn(x)是屬不同的分佈。
上述這些方法與步驟都可以設計成電腦程式,完全由交由個人電腦來執行並下判斷,電腦程式的設計與撰寫並不困難。
肆、範例展示
本文作者已根據第二章所述之理論與數學式,以微軟(Microsoft) Visual Basic程式語言,將KS-test 撰寫成電腦程式,可以在微軟Windows環境下的個人電腦上運跑。本章將利用作者自撰之電腦程來展示兩個範例,以示KS-test之應用結果,這兩個範例都是屬於兩組樣本測試(TST)之案例。
4.1 範例一
範例一之兩組數據組分別如下:
Case-1A={0.22, -0.87, -2.39, -1.79, 0.37, -1.54, 1.28, -0.31, -0.74, 1.72, 0.38, -0.17, -0.62, -1.10, 0.30, 0.15, 2.30, 0.19, -0.50, -0.09}
Case-1B={-5.13, -2.19, -2.43, -3.83, 0.50, -3.25, 4.32, 1.63, 5.18, -0.43, 7.11, 4.87, -3.10, -5.81, 3.76, 6.31, 2.58, 0.07, 5.76, 3.50}
這兩組數據組的平均值都接近零,且數據也大約平衡地散佈在零的兩側,然而Case-1B的數據組則明顯地具有較大變化幅度,從-5.81變化到7.11;而Case-1A的數據組則僅從-2.39變化至2.3而已。因此,這兩組數據組顯然是不同的,但若使用Student’s t-test來進行測試,則無法看出其差別,以KS-Test進行分析的結果示於圖5中。
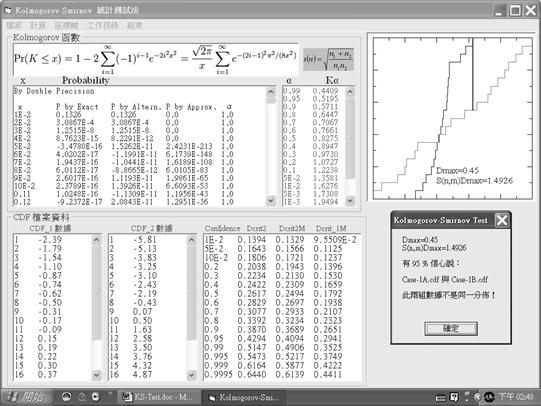
圖5 範例一之KS-test分析結果
圖5畫面右上方的繪圖區顯示出Case-1A與Case-1B之CDF分佈曲線(鋸齒狀曲線者),其中那一道垂直紅線顯示兩CDF分佈曲線間之最大垂直距離與所在位置,其中的文字顯示Dmax=0.45、sn,mDmax=1.4926。圖5畫面中間靠上方有一欄粉紅色表列,顯示α與Kα之對應數值,在α=0.05時,Kα=1.3581,在α=0.01時,Kα=1.6276。由於上述之sn,mDmax(=1.4926)之數值落在α=0.05與α=0.01之間,因此畫面右下方的訊息方塊顯示了「有95%的信心說:Case-1A.cdf與Case-1B.cdf此兩組數據不是同一分佈!」
4.2 範例二
範例二之兩組數據組分別如下:
Case-2A={1.26, 0.34, 0.70, 1.75, 50.57, 1.55, 0.08, 0.42, 0.50, 3.20, 0.15, 0.49, 0.95, 0.24, 1.37, 0.17, 6.98, 0.10, 0.94, 0.38}
Case-2B={2.37, 2.16, 14.82, 1.73, 41.04, 0.23, 1.32, 2.91, 39.41, 0.11, 27.44, 4.51, 0.51, 4.50, 0.18, 14.68, 4.66, 1.30, 2.06, 1.19}
這兩組數據都是取自Log-normal分佈,但平均值不同且相差頗大,由於是非normal分佈數據,故t-test無法看出其差別,但KS-test則可測出其不同!當然若分析人員事先知道這兩組數據是非常態分佈,那麼這位分析師應該知道不能使用Student’s t-test來進行分析,以KS-Test進行分析的結果示於圖6中。
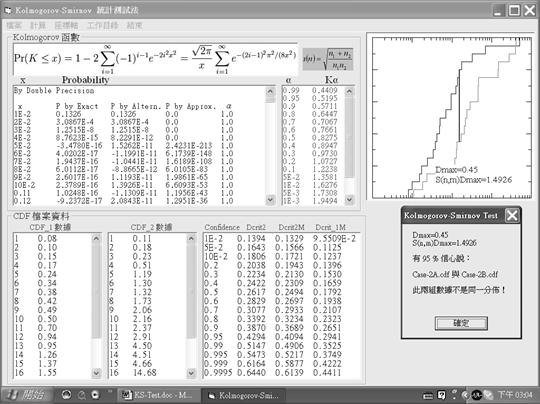
圖6 範例二之KS-test分析結果
圖6之畫面設計與圖5者相同,因為是由同一電腦程式所輸出之畫面的緣故,因此不再贅述畫面上之資訊。由於sn,mDmax(=1.4926)之數值也是落在α=0.05與α=0.01之間,因此畫面右下方的訊息方塊也是顯示了「有95%的信心說:Case-2A.cdf與Case-2B.cdf此兩組數據不是同一分佈!」
伍、結論
本文所介紹之KS-test技術係專門針對分佈型數據組進行統計學上的分析,主要是用來判斷某一數據組是否出自某一參考分佈函數,或用來判斷某兩數據組是否屬相同的分佈。此法其數學並不繁瑣困難,在應用程序上也相當簡單,因此電腦程式容易設計與使用。此法的特點是其強軔性,且不需對數據組的分佈型態預做任何假設,若以圖形顯示分析結果時,可任意選用線性或對數之X-軸尺規。
KS-test非常適合被應用來探討具「不確定性」之評估結果的分析,例如垃圾掩埋場污染物之外釋濃度,或放射性廢棄物(如用過核子燃料(spent nuclear fuel)及低放射性廢棄物(low-level radioactive waste)等)最終處置場外釋核種對人體之劑量率等。由於這些系統的關鍵參數如容器壽命、地下水流速、孔隙率(porosity)、吸附係數等等,其數值都具有相當的不確定性,因此評估所得結果常以CDF方式來表示,不同的情節(scenario)會得到不同的CDF曲線,可以用 KS-test 技術來分析這些CDF曲線,判斷參數對系統的影響程度。
陸、參考文獻
1. Andrade, F. A., I. Esat, and M. N. M. Badi, 2001, “A New Approach to Time-Domain Vibration Condition Monitoring: Gear Tooth Fatigue Crack Detection and Identification by the Kolmogorov-Smirnov Test”, Journal of Sound and <ibration () 240(5), 909-919.
2. Chen, Min and Hong, Zhi An, 1997, “A Kolmogorov-Smirnov Type Test for Conditional Heteroskedasticity in Time Series”, Statistics and Probability Letters, 33, 321-331.
3. Drew, John H. Andrew G. Glen, and Lawrence M. Leemis, 2000, “Computing the cumulative distribution function of the Kolmogorov-Smirnov statistic”, Computational Statistics & Data Analysis 34, 1-15.
4. Fasano, G. and Franceschini, A., 1987, “A Multidimensional Version of the Kolmogorov-Smirnov Test”, Mon. Not. R. Astr. Soc., 225, 155-170.
5. Greenwell, Raymond N and Stephen J. Finch, 2004, “Randomized Rejection Procedure for the Two-sample Kolmogorov–Smirnov Statistic”, Computational Statistics & Data Analysis 46, 257-267.
6. Justal, Ana, Daniel Pana, and Ruben Zamar, 1997, “A Multivariate Kolmogorov-Smirnov Test of Goodness of Fit”, Statistics and Probability Letters, 35, 251-259.
7. Kar, Chinmaya and A.R. Mohanty, 2006, “Multistage gearbox condition monitoring using motor current signature analysis and Kolmogorov–Smirnov test”, Journal of Sound and Vibration, 290, 337-368.
8. Meintanis, Simos G., 2007, “A Kolmogorov–Smirnov type test for skew normal distributions based on the empirical moment generating function”, Journal of Statistical Planning and Inference, 137, 2681-2688.
9. Wikipedia, the free encyclopedia, 2009,
http://en.wikipedia.org/wiki/Kolmogorov%E2%80%93Smirnov_test
10. Young, Ian T., 1977, “Proof without Prejudice: Use of the Kolmogorov-Smirnov Test for the Analysis of the Histograms from Flow Systems and Other Sources”, The Journal of Histochemistry and Cytochemistry, 25(7), 935-941.