陳智隆 賴仁杰
核能研究所 榮福股份有限公司
摘要
核種傳輸是影響放射性廢棄物處置場安全性的關鍵議題。本研究從安全評估的觀點,根據脈衝源一維、二維和三維無限邊界與半無限邊界的濃度解析,探討放射性核種在傳輸途徑固定位置(x=xo)上的最大濃度,與其對應時間的解析。並對放射性核種最大濃度的對應時間進行距離、流速與延散度的參數敏感度分析。結果顯示放射性核種最大濃度的對應時間受距離影響主要在短距離內,且在短距離內受流速影響亦較大,而放射性核種最大濃度對應時間則對延散度最為敏感。研究成果有助於我國放射性廢棄物最終處置場安全評估技術之提升。
關鍵詞(Key Words) :脈衝源(impulse source) 、解析解(analytical solution) 、最大濃度(maximum concentration) 、對應時間(responding time) 、參數敏感度(parameter sensitivity)
壹、前言與目的
我國低放射性廢棄物最終處置設施安全分析報告導則 22,說明處置設施經營者申請低放射性廢棄物最終處置設施建造執照時,所附安全分析報告內容,應依處置設施之綜合概述;場址之特性描述;設施之設計;設施之建造;設施之運轉;設施之安全評估;設施之組織規劃、行政管理及人員訓練計畫;輻射防護作業及環境輻射監測計畫;保安計畫、意外事件應變計畫及消防防護計畫;最終處置設施封閉及監管規劃;品質保證計畫及其他經主管機關指定之事項等重要事項規劃章節詳加說明。
其中,處置設施安全評估之正常狀況或異常狀況輻射劑量評估,應說明:評估處置設施運轉期間及封閉後在正常狀況下或意外事故/異常狀況下之輻射劑量,包括傳輸機制說明、情節分析、輸入資料、輸出資料、敏感度分析、不確定性分析、評估結果及使用之評估程式,以及核種外釋到達人類活動範圍之傳輸機制等。故此,為能符合最終處置設施安全分析報告導則之要求,需進行最終處置場全系統輻射劑量瞭解,以評估不同狀況下,核種可能對人類造成之最大劑量是否符合法規要求。
最終處置場全系統輻射劑量評估,包括核種可能外釋後的廢棄物容器表面活度、通過工程障壁後的活度、通過地質圈後的活度,以及最重要的是對生物圈影響人類可能造成之最大輻射劑量率。
廢棄物容器表面活度主要受廢棄物容器壽命決定,一般皆保守假設在處置後廢棄物容器隨即破壞。工程障壁對核種的隔離與阻絕有一定時效,但仍遠低於劑量評估的考量時間。另外處置場使用的區域相對於所需評估的地質圈範圍(包括核種外釋途徑或劑量評估範圍)亦較小,因此可合理簡略假設核種以脈衝源型式從處置場外釋。此外,若再考量處置場岩層為均勻物質,則對複雜的處置場全系統輻射劑量評估而言,便可藉由簡單的脈衝源解析推估核種外釋後通過地質圈的最大濃度值與其對應時間,進而評估主要人類群體可能受到的最大輻射劑量率,因此如何推算脈衝源解析的核種最大濃度值與其對應時間(即發生最大濃度值之時間)為最基本且重要的研究課題。
基於上述安全分析考量之條件,本研究即針對此課題運用三個不同維度的脈衝源解析解,分析其核種最大濃度與其對應的時間,並進行核種最大濃度對應時間的參數敏感度分析,以瞭解不同傳輸參數對核種最大濃度與其對應時間的影響程度。
貳、文獻回顧
諸多文獻 1, 2, 4, 8, 14, 19皆僅分別列出解析解的形式或探討不同邊界和源項條件的解析解的形式 11, 13, 15, 17, 18。其他則分別進行一維與二維無限與半無限邊界脈衝源數值解形式與解析解的比較 5;兩個無因次化三維質傳方程式比較 10;以及三維半無限定濃度邊界條件下沿主要水流方向的最大濃度探討 7。而探討核種遷移最大濃度特性的相關文獻,主要有 Yu20發展的分析低放射性廢棄物處置場或化學廢棄物掩埋場對環境衝擊的電腦評估模式,其報告中探討源項特性時,曾推估子核種的一階瀝濾(Leaching)下的最大濃度與其發生時間。Rogers 16解析核種通過吸附介質時的最大濃度與流量關係式,並以此關係式探討濃度重布效應(Reconcentration Effort) 。其關係式主要由一維核種傳輸控制方程式出發,考量吸附作用,但忽略延散作用,可求得母核種與子核種的最大濃度變化,並得知母核種最大濃度主要受傳輸時間(至距離 x 的時間)內的衰變作用影響,而子核種最大濃度變化,當子核種的吸附係數小並較半化期短時,則傳輸距離超過某特定值時,子核種活度可能大於母核種活度。
Yu(1987)20的研究僅包括全系統輻射劑量評估的源項部份探討;Rogers(1978)16則簡略了地下水核種傳輸重要的延散作用。本研究考量了延散作用及衰變作用的一維、二維與三維無限邊界和半無限邊界脈衝源解析解(如表 1 所列) ,運用假設的參數探討不同維度之間,在特定位置(即核種外釋到達人類活動範圍)核種發生最大濃度與時間的差異。
表 1 一維、二維與三維無限邊界和半無限邊界脈衝源解析解
| |
解析解 |
文獻 |
方程式
編號 |
| 1-D |
(A) |
M (x-υt)2
C(x,t)= exp(- - λt)
nA(4πtDx)1/2 4Dxt
|
6 |
(1-1) |
| (B) |
Mx (x-υt)2
C(x,t)= exp(- - λt)
υtnA(4πtDx)1/2 4Dxt |
21 |
(1-2) |
| 2-D |
(A) |
M (x-υt)2 y2
C(x,y,t)= exp(- - - λt)
nb4πt(DxDy)1/2 4Dxt 4Dyt |
9 |
(1-3) |
| (B) |
Mx (x-υt)2 y2
C(x,y,t)= exp(- - - λt)
υtnb4πt(DxDy)1/2 4Dxt 4Dyt |
12 |
(1-4) |
| 3-D |
(A) |
M (x-υt)2 y2 z2
C(x,y,z,t)= exp(- - - - λt)
8n(π3t3DxDyDz)1/2 4Dxt 4Dyt 4Dzt |
6 |
(1-5) |
| (B) |
Mx (x-υt)2 y2 z2
C(x,y,z,t)= exp(- - - - λt)
8υtn(π3t3DxDyDz)1/2 4Dxt 4Dyt 4Dzt |
21 |
(1-6) |
註:(A)為無限邊界、(B)為半無限邊界
符號說明:
C(x,t):在觀測位置(x)並傳輸時間(t)的一維傳輸核種濃度[M/L3]
C(x,y,t):在觀測位置(x,y)並傳輸時間(t)的二維傳輸核種濃度[M/L3]
C(x,y,z,t):在觀測位置(x,y,z)並傳輸時間(t)的三維傳輸核種濃度[M/L3]
υ :均勻流場中的地下水平均流速[L/T]
Dx:x 方向延散係數[L2/T], Dx = υαx + Dd
αx :x 方向延散度[L]
Dd :擴散係數[L2/T]
M :脈衝注入的核種質量[M]
A :垂直水流方向的截面積[L2]
n :孔隙率[-]
Dy :y 方向延散係數[L2/T],Dy = υαy + Dd
αy :y 方向延散度[L]
b :含水層厚度[L]
Dz :z 方向延散係數[L2/T], Dz = υαz + Dd
αz :z 方向延散度[L]
與本議題最直接相關的是 Bedient et al. 3的研究,其針對三維無限脈衝源提出當時間 t=to(即 t=x/υ)時,沿主要水流方向的最大濃度(C3Dmax)為 C3Dmax = COVO / [ 8(π3t3DxDyDz)1/2 ]
其中
Co :注入濃度[M/L3]
Vo :注入核種之含水層單位孔隙體積[L3]
υ :均勻流場中的地下水平均流速[L/T]
Dx :x 方向延散係數[L2/T], Dx = υαx + Dd
Dy :y 方向延散係數[L2/T], Dy = υαy + Dd
Dz :z 方向延散係數[L2/T], Dz = υαz + Dd
並在其案例中定義二維無限邊界脈衝源解析解的最大濃度(C2Dmax)為 C2Dmax = COAO / [ 4πt(DxDy)1/2 ]
其中
Ao :注入核種之含水層單位孔隙面積[L2]
比較式(1)與表 1 中式(1-5)可知 Co * Vo = M / n 。比較式(2)與表 1 中式(1-3)可知Co * Ao = M / nb。假設x=υt、y=0與z=0,代入表1中式(1-5),可得到Bedient et al. 3的三 維無限邊界脈衝源解析解的最大濃度(C3Dmax)式(1),並且相似的 x=υt 與 y=0 情況,則由表 1 中式(1-3)可得到式(2)。Bedient et al.的最大濃度乃討論在某時間點(to)時,在空間分佈上存在的最大濃度。然而,就安全評估的觀點而言,關心的是關鍵受體接受到的最大濃度值,亦即受體接受的最大濃度值乃是以在受體所在位置(xo)曾經發生過的最大濃度,按此定義最大濃度並非發生在 x= υ t 時的濃度,而是發生於 當 x=xo 之 dC/dt=0 的濃度,故此最大濃度與其對應時間為本研究的主要探討問題。
參、推算最大濃度與對應時間
如前節所述,受體接收之最大濃度為 dtdC = 0 時的濃度,且最大濃度必發生在沿著主要水流方向上(即 y=0 與 z=0) 。根據此定義將表 1 中式(1-1)~式(1-6)對時間微分並假設為 0,則可得到一維、二維與三維無限邊界和半無限邊界最大濃度與對應時間(列於表 2 中) 。以下便針對不同維度下的最大濃度與對應時間進行探討,首先在不考慮衰變作用的情形下,將結果與 Bedient et al.的案例進行比較,以瞭解前述在某時間點(to)空間分佈上的最大濃度,與在固定位置(xo)發生的最大濃度之間的差異。

一、未考慮衰變作用
(一)一維情形
使用的參數值參考自 Bedient et al. 3案例 6.2。其參考參數分別為平均流速(υ)為 1.0 m/day,注入質量(M)為 105 g,x, y, z 方向的延散係數(Dx, Dy, Dz)分別為 1.0 m, 0.1 m, 0.1m,並以三個不同距離(75 m, 200m, 400m)進行比較。 根據上述參數條件不考慮衰變作用,代入表 2 式(2-1)與式(2-2)可得一維無限邊界與半無限邊界濃度分佈情形如圖 1 所示。由圖 1 可看出 C1DmaxI < C1DmaxS 並 t1DmaxI > t1DmaxS。C1DmaxI 分別為 3268.2 g/m3, 1785.9 g/m3與 1411.4 g/m3,對應的時間 t1DmaxI 則分別為 74.0 day, 249.0 day 與 399.0 day;而 C1DmaxS 為 3356.5 g/m3, 1800.3 g/m3與 1418.4 g/m3,t1DmaxS 為 72.1 day, 247.0 day 與 397.0 day。
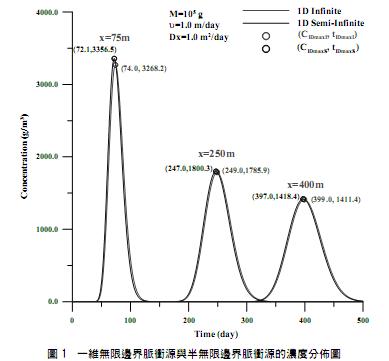
(二)二維情形
1. 二維無限邊界
使用相同的參數條件分別計算三個不同距離(75 m, 200m, 400m)的濃度分佈情形並與 Bedient et al.案例 6.2 之式(2)比較,結果示於圖 2。以式(2)分別計算距離為 75 m, 200 m 和 400 m 時的最大濃度為 335.5 g/m3, 100.7 g/m3與62.9 g/m3, 對應的時間分別為 75.0 day, 250.0 day 與 400.0 day,由圖 2 可看出式(2)的計算結果與此研究的結果並不相同,此乃因 Bedient et al.立基於t=to,而本研究立基於 x=xo。本研究求得之最大濃度與其對應時間依據表2 式(2-3),最大濃度分別為 340.0 g/m3, 101.1 g/m3與 63.1 g/m3,對應的時間分別為 73.0 day, 248.0 day 與 398.0 day。
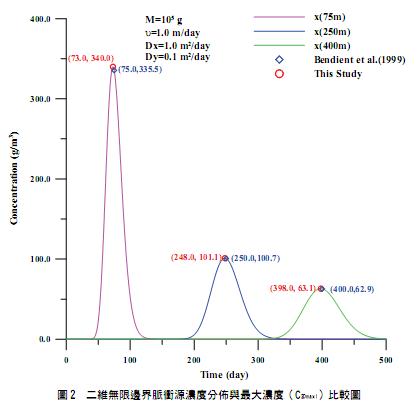
2. 二維半無限邊界
二維半無限邊界情形在使用相同的參數條件下,亦分別計算三個不同距離(75 m, 200m, 400m)的濃度分佈情形如圖 3 所示。最大濃度與對應時間計算結果分別為 353.9 g/m3, 102.3 g/m3與 63.5 g/m3,對應的時間分別為 71.1 day, 246.0 day 與 396.0 day,此結果亦比二維無限邊界情形的濃度值略高且對應時間約減少 2 day。
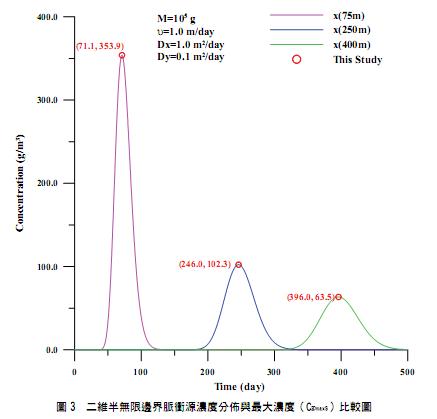
(三)三維情形
1. 三維無限邊界
三維無限邊界濃度分佈情形如圖 4 所示。若以式(1)分別計算距離為 75 m, 200 m 和 400 m 時的最大濃度分別為 34.6 g/m3, 5.7 g/m3與 2.8 g/m3,對應的時間分別為 75 day, 250 day 與 400 day,但由圖 4 可看出式(1)的計算結果並非最大濃度與其對應時間,最大濃度與對應時間應為表 2 式(2-5),其計算結果最大濃度分別為 35.6 g/m3, 5.7 g/m3與 2.8 g/m3,對應的時間分別為 72.1 day, 247.0 day 與 397.0 day。
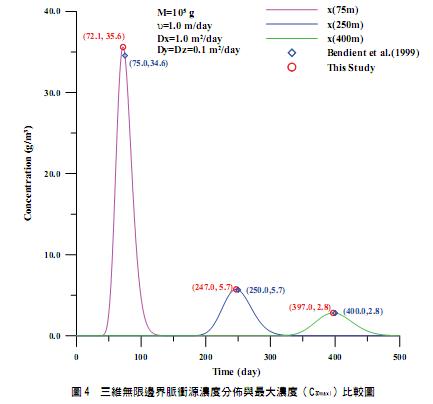
2. 三維半無限邊界
三維半無限邊界濃度分佈情形如圖 5 所示。以表 2 式(2-6)計算最大濃度與對應時間分別為 37.6 g/m3, 5.8 g/m3與 2.9 g/m3,對應的時間分別為 70.2 day, 245.1 day 與 395.0 day,此結果比三維無限邊界情形的濃度值略高且對應時間約減少 2 day。將上述一維、二維與三維的最大濃度與對應時間計算結果彙整於表 3,由表3 可看出半無限邊界或無限邊界最大濃度發生時間依序為三維、二維與一維,且半無限邊界條件的發生時間皆早於無限邊界條件,另外,三維無限邊界條件的最大濃度發生時間會等於一維半無限邊界條件的最大濃度發生時間,此現象亦可由比較表 2 式(2-5)與式(2-2)得證。
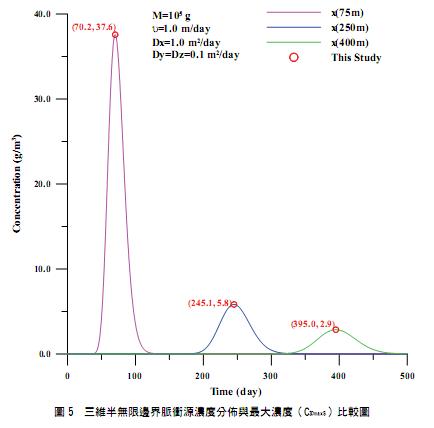
表 3 不同距離(75m, 250m, 400m)一維、二維與三維無限邊界和半無限邊界最大濃度與對應時間彙整表
| |
|
x=75m |
x=250m |
x=400m |
| 一維 |
無限邊界 |
t1DmaxI
|
74.0 |
249.0 |
399.0 |
| C1DmaxI |
3268.2 |
1785.9 |
1411.1 |
| 半無限邊界 |
t1DmaxS |
72.1 |
247.0 |
397.0 |
| C1DmaxS |
3356.5 |
1800.3 |
1418.4 |
| 二維 |
無限邊界 |
t2DmaxI |
73.0 |
248.0 |
398.0 |
| C2DmaxI |
340.0 |
101.1 |
63.1 |
| 半無限邊界 |
t2DmaxS |
71.1 |
246.0 |
396.0 |
| C2DmaxS |
353.9 |
102.3 |
63.5 |
| 三維 |
無限邊界 |
t3DmaxI |
72.1 |
247.0 |
397.0 |
| C3DmaxI |
35.6 |
5.7 |
2.8 |
| 半無限邊界 |
t3DmaxS |
70.2 |
245.1 |
395.0 |
| C3DmaxS |
37.6 |
5.8 |
2.9 |
單位:day, g/m3
二、考慮衰變作用
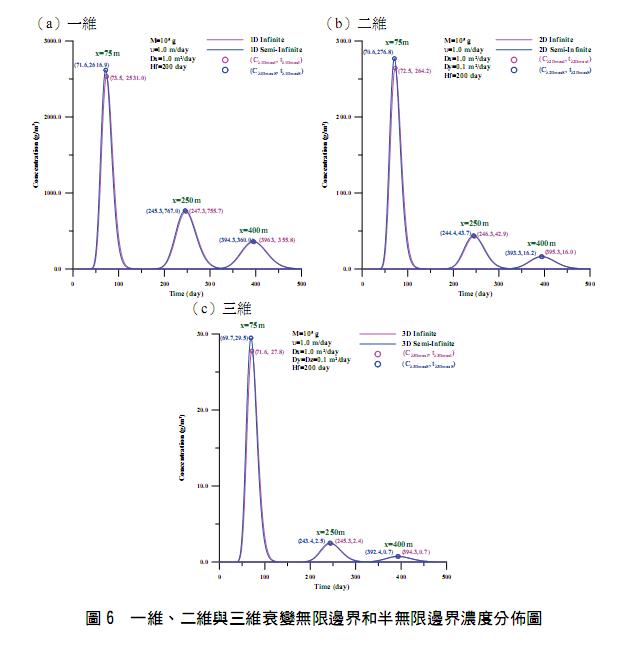
使用與前述相同的參數條件並半衰期為 200 day,分別計算三個不同距離(75 m, 200m, 400m) 的一維、二維與三維衰變無限邊界和半無限邊界的濃度分佈情形。圖 6(a)為一維衰變無限邊界和半無限邊界濃度分佈、圖 6(b)為二維衰變無限邊界和半無限邊界濃度分佈而圖 6(c)為三維衰變無限邊界和半無限邊界濃度分佈。由圖 6 可知無限邊界最大濃度皆低於半無限邊界最大濃度,且其對應時間亦較大。將三個不同距離的模擬結果彙整於表 4 中,表 4 亦可看出與表 3 相似的結果:半無限邊界或無限邊界最大濃度發生時間依序為三維、二維與一維,且半無限邊界條件的發生時間皆早於無限邊界條件;三維無限邊界條件的最大濃度發生時間會等於一維半無限邊界條件的最大濃度發生時間。
表 4 不同距離(75m, 250m, 400m)一維、二維與三維衰變無限邊界和半無限邊界最大濃度與對應時間彙整表
| |
|
x=75m |
x=250m |
x=400m |
| 一維 |
無限邊界 |
tλ1DmaxI
|
73.5 |
247.3 |
396.3 |
| Cλ1DmaxI |
2531.0 |
755.7 |
355.8 |
| 半無限邊界 |
tλ1DmaxS |
71.6 |
245.0 |
394.3 |
| Cλ1DmaxS |
2616.9 |
767.0 |
360.0 |
| 二維 |
無限邊界 |
tλ2DmaxI |
72.5 |
246.3 |
395.3 |
| Cλ2DmaxI |
264.2 |
42.9 |
16.0 |
| 半無限邊界 |
tλ2DmaxS |
70.6 |
244.4 |
393.3 |
| Cλ2DmaxS |
276.8 |
43.7 |
16.2 |
| 三維 |
無限邊界 |
tλ3DmaxI |
71.6 |
245.3 |
394.3 |
| Cλ3DmaxI |
27.8 |
2.4 |
0.7 |
| 半無限邊界 |
t3DmaxS |
69.7 |
243.4 |
392.4 |
| C3DmaxS |
29.5 |
2.5 |
0.7 |
單位:day, g/m3
另外,比較表 4 與表 3 的結果可知考慮衰變情形時,除最大濃度值會因衰變作用而減低外,其發生時間亦會提前,此現象乃由於衰變作用導致最大濃度下降,因此若在相同時間點上相較於未考慮衰變作用的濃度值,其最大濃度值時間勢必要提前以達到最佳平衡,故考慮衰變作用時的最大濃度時間會較無衰變作用的最大濃度時間低。 相同道理亦可解釋為何三維情形的最大濃度時間會低於二維情形或一維情形,其亦由於三維或二維情形相較於一維情形在其他維度上猶如衰變作用般減低主水流方向上的濃度值,而三維比二維多一個維度,其濃度損失現象更為明顯,因此在探討主水流方向上的最大濃度發生時間上,勢必三維情形要比二維情形提早而比一維情形更為提早,方能達到最佳平衡。由以上討論可知,最大濃度發生時間是一個值得深入討論的議題,以下即對此議題進行最大濃度發生時間參數敏感度分析。
肆、最大濃度對應時間參數敏感度分析
一、距離(x)敏感度
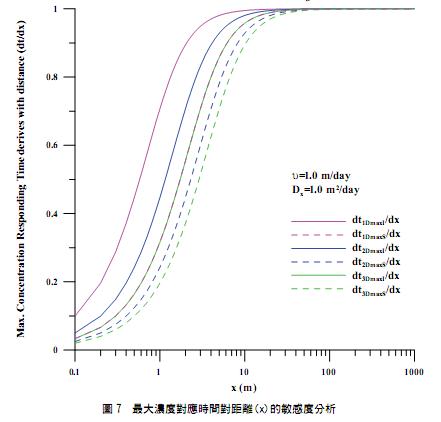
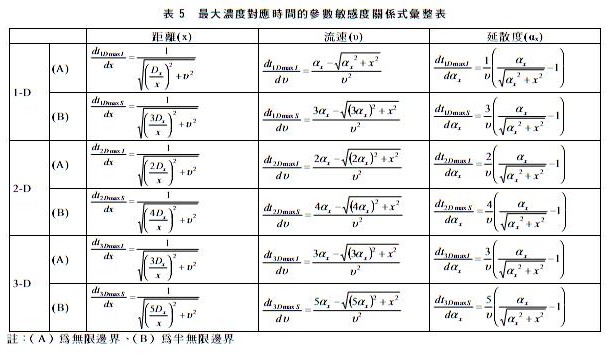
不考慮衰變作用下,將表 2 中最大濃度對應時間對距離(x)微分,可得到最大濃度對應時間的距離敏感度關係式(列於表 5 中) 。以 Dx=1.0 m2/day 和 υ=1 m/day 探討最大濃度對應時間對距離(x)的敏感度分析作圖於圖 7。由圖 7 可看出,最大濃度對應時間受距離影響主要在短距離內,且依序以一維無限邊界(dt1DmaxI/dx) 、二維無限邊界(dt2DmaxI/dx) 、三維無限邊界(dt3DmaxI/dx)=一維半無限邊界(dt1DmaxS/dx) 、二維半無限邊界(dt2DmaxS/dx) 、三維半無限邊界(dt3DmaxS/dx)最快達到定值,此定值可由表 5 中距離敏感度關係式,假設 ∞ → x 而推導得該定值為1/υ。
二、流速(υ)敏感度
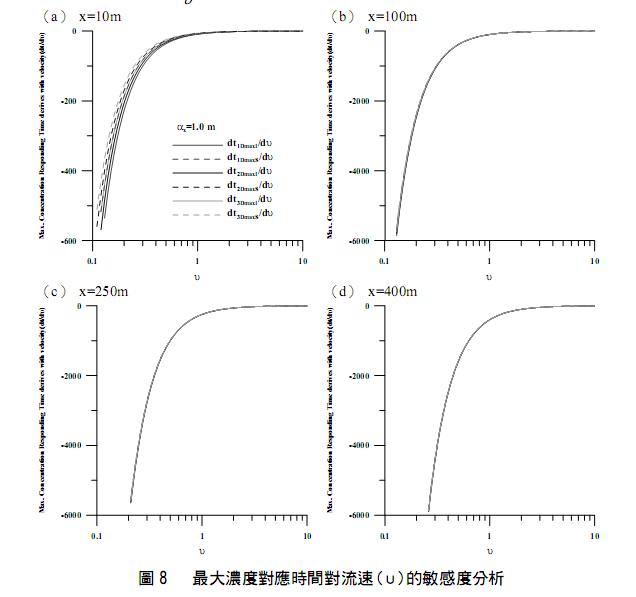
因為 Dx=αxυ+Dd,而 Dd 一般遠小於 αxυ,故可假設 Dx ≈ αxυ。不考慮衰變作用下,將表 2 中最大濃度對應時間對流速(υ)微分,可得到最大濃度對應時間的流速敏感度關係式(亦列於表 5 中) 。 以 αx=1.0 m 和四個不同距離(10m, 100m, 250m, 400m)探討最大濃度對應時間對流速(υ)的敏感度分析如圖 8 所示。由圖 8 可看出在小距離內(圖 8(a))最大濃度對應時間受流速影響較敏感,而距離較大後(圖 8(b)、圖 8(c)、圖 8(d)) ,流速敏感度趨於一致,此意指在某固定距離上,流速愈快則不同維度造成的濃度稀釋作用或延散作用愈小;由表 5 中流速敏感度關係式可知,關係式的分母為常數,在距離為定值(即固定位置)時,則最大濃度對應時間的流速敏感度正比於1/υ2,其積分結果可知最大 濃度對應時間將正比於1/υ,並與最大濃度對應時間的距離敏感度分析結果一致。
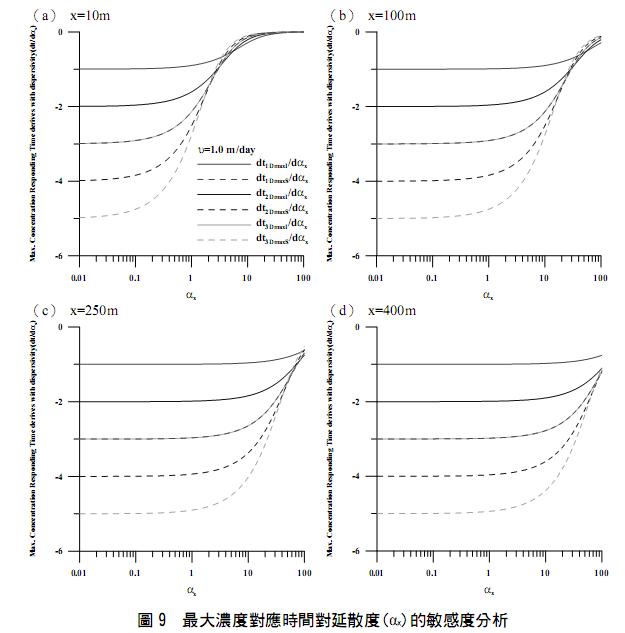
三、延散度(αx)敏感度
依前節相同假設 Dx ≈ αxυ,不考慮衰變作用下,將表 2 中最大濃度對應時間對延散度(αx)微分,可得到最大濃度對應時間的延散度敏感度關係式(亦列於表 5 中) 。 以 υ=1.0 m/day 和四個不同距離(10m, 100m, 250m, 400m)探討最大濃度對應時間對延散度(αx)的敏感度分析作圖於圖 9。由圖 9 可看出(A)延散度較小或很大時,最大濃度對應時間敏感度趨於定值;(B)高敏感度範圍受不同距離影響,距離愈大則高敏感度範圍延散度的值愈大,意指距離愈大時延散度(αx)要愈大方能對最大濃度對應時間產生影響;(C)半無限邊界條件的敏感度範圍大於無限邊界條件,且維度愈高其敏感度範圍亦愈大;(D)比較圖7、圖8與圖9可知,最大濃度對應時間對延散度最為敏感。
伍、結論與建議
藉由以上一維、二維與三維無限邊界與半無限邊界脈衝源最大濃度與對應時間的分析,可歸納出以下幾點結論:
一、以安全評估的觀點,在固定受體位置(即 x=xo)上,一維、二維與三維無限邊界與半無限邊界脈衝源最大濃度分佈方程式(見表 2) ,與 Bedient et al.以固定時間(t=to),在空間分佈上最大濃度之式(1)或式(2)並不相同;一維、二維與三維無限邊界與半無限邊界脈衝源最大濃度對應時間亦非為 υ x 。
二、藉由一維、二維與三維無限邊界與半無限邊界脈衝源最大濃度對應時間的距離、流速與延散度的敏感度分析可知,最大濃度對應時間受距離影響主要在短距離內且在短距離內受流速影響亦較大,而最大濃度對應時間對延散度最為敏感。
由以上研討可知最大濃度對應時間受延散度的影響最大,相對的其亦影響最大濃度,因此就處置場安全評估的觀點而言,當進行現地實驗參數調查時,需特別注意此參數的調查精度與技術。
陸、參考文獻
1. Bear, J., 1972, Dynamic of Fluids in Porous Media, American Elsevier, New York, 764p.
2. Bear, J., 1979, Hydraulic of Groundwater, McGraw-Hill, Inc., 569p.
3. Bedient, P.B., H.S. Rifai and C.J. Newell, 1999, Ground water contamination: transport and remediation, PTR Prentice-Hall, Inc., 603p.
4. Bauer, P., S. Attinger and W. Kinzelbach, 2001, Transport of a decay chain in homogeneous porous media: analytical solutions, Journal of Contaminant Hydrology, Vol.49, p.217-239.
5. Carlier, E., 2008, Analytical solutions of the advection-dispersion equation for transient groundwater flow. A numerical validation, Hydrological Processes, p.3500-3506.
6. Crank, J., 1956, The Mathematics of diffusion, Oxford University Press. 414p.
7. Domenico, P.A., 1987, An analytical model for multidimensional transport of a decaying contaminant species, Journal of Hydrology, Vol.91, p.49-58.
8. Freeze, R.A. and J.A. Cherry, 1979, Groundwater, Prentice-Hall Inc., Englewood Cliffs, N.J., 604p.
9. Fried, J.J., 1975, Groundwater Pollution, Elsevier.
10. Guyonnet, D. and C. Neville, 2004, Dimensionless analysis of two analytical solutions for 3-D solute transport in groundwater, Journal of Contaminant Hydrology, Vol.75,p.141-153.
11. Kreft A. and A. Zuber, On the physical meaning of the dispersion equation and its solutions for different initial and boundary conditions, Chemical Engineering Science, 1978, Vol. 33, p.1471-1480.
12. Lenda, A. and A. Zuber, 1970, Tracer dispersion in groundwater experiments, Proceedings of Symposium Isotope Hydrology, IAEA, Vienna. SM 129/37, p.619-641.
13. Lindstrom, F.T. and L. Boersma, 1989, Analytical Solutions for Convective-Dispersive Transport in Confined Aquifers with Different Initial and Boundary Conditions, Water Resource Research, Vol.25, No.2, p.241-256.
14. Luckner L. and W.M. Schestakow, 1991, Migration Processes in the Soil and Groundwater Zone, LEWIS PUBLISHERS, INC., 485p.
15. Park, E. and H. Zhan, 2001, Analytical solutions of contaminant transport from finite one-, two-, and three-dimensional source in a finite-thickness aquifer, Journal of Contaminant Hydrology, Vol.53, p.41-61.
16. Rogers, V.C., 1978, Migration of Radionuclide chains in groundwater, Nuclear Technology, Vol.40, p.315-320.
17. Shan, C. and I. Javandel, 1997, Analytical solutions for solute transport in a vertical aquifer section, Journal of Contaminant Hydrology, Vol.27, p.63-82.
18. Sim, Y. and C.V., Chrysikopoulos, 1999, Analytical solutions for solute transport in saturated porous media with semi-infinite or finite thickness, Advances in Water Resources, Vol.22, No.5, p.507-519.
19. Todd, D.K. and L.W. Mays, 2005, Groundwater Hydrology, John Wiley & Sons, Inc., 636p.
20. Yu, C., 1987, Modeling of Low-Level-Waste disposal for Environmental impact analysis, Argonne National Lab., CONF-870306-70.
21. Zuber, A., 1974, Theoretical possibilities of two-well pulse method, Isotope Techniques in Groundwater Hydrology, Vol.2, p.277-294.
22. 行政院原子能委員會,2004,低放射性廢棄物最終處置設施安全分析報告導則,會物字第 09300036761 號函。