張明儒 杜炎勳 蔡柏軍
原子能委員會核能研究所
摘 要
壓力管線因劣化而導致洩漏，甚至是斷裂的問題，一直以來都是運轉中核能電廠最關心的議題之一，為了確保管線結構的完整性，研究其安全評估方法，十分具有工程應用上的價值。然而，J-積分便是其中一種用以判別裂縫是否擴展的重要物理量。本研究利用有限元素軟體「ABAQUS」，針對含圓周向穿壁裂縫直管，分別承受軸向拉力和彎矩作用下，建立三維的彈塑性有限元素模型，計算分析J-積分值，並探討材料性質與幾何參數改變對J-積分值的影響。計算結果發現，裂縫愈長，J-積分值愈大，裂縫就愈容易擴展。另外，彎矩作用對長裂縫管線的影響非常明顯，長短裂縫的J-積分值有很大的差異，此點是與受軸向拉力的案例最大的不同處。
關鍵詞︰先漏後破、J-積分、穿壁裂縫、管線。
壹、前言
一、研究背景
壓力容器及管線廣泛應用於石油、化工、航太、能源、冶金等重要工業，是工業製造過程中必要的元件，影響著國家經濟的脈動。壓力容器及管線長時間暴露於高侵蝕性、高溫、高壓、易燃、易爆的環境，萬一發生爆裂，將會造成嚴重的工安事故，導致生產停溜和國家經濟衰退，進而使人民的生命財產蒙受巨大損失，直接影響社會的安定。自從台灣進入工業化以來，管線的應用發展迅速，其中又以石油、天然氣、能源的管線運輸系統最長、最複雜又最危險。以石油的管線為例，若煉油廠一條輸油管破裂，原油流入河川或海洋，綿延數十公里的污染原油，將會造成生態浩劫。以核能電廠為例，核能電廠經過多年運轉，結構組件開始老化、劣化，對電廠的元件而言，不允許構件因裂縫突然快速擴展，而產生失控的情況。例如，PWR內之蒸氣產生器其內部之管束為主系統壓力邊界，造成管束劣化除了主要的原因-「凹陷」之外，還有管壁薄化、沖腐蝕、疲勞、磨耗、孔蝕、晶界侵蝕、應力腐蝕裂縫等因素，皆會造成管束損壞；管束損壞時，會高壓主水過量洩漏到低壓二次側，因而停機使供電量下降，勢必會有經濟損失。另外，例如，再循環管線以及爐心噴灑管線焊道即曾於大修時檢測出裂縫，管線及壓力容器的爆裂事件常常與焊接缺陷相關；由此看來，壓力管線作為一種典型的焊接結構，其焊接過程常常使焊接接頭的組織性能劣化及產生缺陷，在焊接缺陷處有較大的應力集中，在使用過程中往往成為裂縫的起始點。然而，管線一旦從焊接接頭處發生斷裂，極易造成突發性和災難性斷裂。
大部分的壓力構件因製造過程品質控管的關係，或多或少都可能存在著結構性缺陷，以及使用過程所產生的裂縫和腐蝕等問題。若壓力管線管壁厚度較薄，容易變形，其破壞方式大都為延性破裂，呈現先漏後破( Leak Before Break，LBB )的現象，然而，壓力容器厚度較大，力學行為近似平面應變，故破壞方式較有可能出現低應力脆性斷裂。管線系統所承受的應力方式，通常是較為複雜的組合載重( combined load )，如軸向力( axial force ) 、彎矩( bending moment )、扭轉( torsion )等作用同時發生。因此，工業管線中存在大量的缺陷，其存在往往會成為某些事故的潛在原因，有必要進行深入的研究，提出合理的處理方法。如何評估和處置這些管線，使得既能保證安全生產，又能把維修量降至業界可接受的程度，是工程上急需解決的技術難題，也是政府制定壓力管線檢驗與驗收相關法規必需考慮的關鍵問題。為確保含缺陷壓力管線的安全運行，研究掌握壓力管線缺陷的成因、失效模式、塑性極限承載能力，建立缺陷壓力管線安全評估工程方法，不僅具有重要的理論意義，而且具有重要的工程應用價值。
ASME規範第XI章，對經過運轉階段含裂縫之鋼材管路，依其材質特性之差異大致有三種破壞模式[1~4]，分別為全截面塑性變形、延性撕裂及脆性斷裂，其破壞之評估方式，應分別以極限載重法( Limit Load )、彈塑性破壞力學( Elastic-Plastic Fracture Mechanics, EPFM )，與線彈性破壞力學( Linear-Elastic Fracture Mechanics, LEFM )為理論依據進行評估。傳統的評估方法中，只要表面裂縫貫穿管壁，則判定壓力管線立即失效。先漏後破( LBB )法比傳統的評估法更加精確且更經濟。LBB評估法的主要兩個重要的參數，一是J-積分，從能量的釋放的觀點，進而觀察裂縫成長趨勢；另一則是COD( Crack Opening Displacement )（即裂縫尖端的裂縫面所張開的位移量），當裂縫貫穿後，經由量測裂縫面所張開位移，亦可作為管線是否失效的依據。本研究即以J-積分來探討含穿壁裂縫直管，分別承受軸向力與彎矩作用下，管線的力學行為。
二、文獻回顧
世界先進國家自1970年代開始進行管線元件研究，進入1980年代後，各國在既有的研究基礎上，以及核能發電產業的支持下，美國、日本、德國、英國等國家積極致力於劣化管線的研究，這些研究獲得的成果和經驗，不僅可以應用於核能產業，更可依此制訂相關的法規，以進一步確保管線結構的完整性。自1983 年起國際間陸續有合作計劃研究管路裂縫行為，重點包含管路彈塑性材料特性探討、破壞力學分析、洩漏率評估以及洩漏率量測技術。首先，美國的劣化管線研究計畫(Degraded Piping Program, DPP ) (1984一1989) [5, 6]主要探討含長裂縫管路在準靜態負載下的破裂行為與極限載重，研究內容包括破裂力學分析方法，材料性能測試和全尺寸裂縫管線的斷裂試驗。在這些管線研究的基礎上，ASME規範SECTION XI Division 1特別要求運轉中檢查規定、與劣化設備組件或管路安全評估和維修或汰舊換新準則：IWB 3640及非強制性附錄C(Non-mandatory Appendix C, 適用於不鏽鋼管路裂縫分析) [7]和IWB 3650及非強制性附錄H(Non-mandatory Appendix H, 適用於碳鋼管路裂縫分析) [8]。IWB-3640 詳細規定了有問題的管路裂縫之解析式評估理念、方法，與步驟。決定含裂縫管路是否繼續使用的原則是:確保於下次檢修前預估最後裂縫深度與長度或應力小於規範規定之允許值。預估最後裂縫深度與長度，應包括已檢測出裂縫及未來裂縫成長之預測值，後者與(1)結構所承受外力大小、型態，(2)材料本身之強度與韌度，和(3)結構破壞模式有絕對的關係。然而，規範內附錄C與附錄H都是以應力為主的簡化式的彈塑性破壞力學分析法，這跟本研究所要介紹的以裂縫尖端J積分為主的彈塑性破壞力學分析法，是有所不同。值得注意的是，上述附錄C與H均非強制性的，若是運轉電廠的擁有者，能夠提出另一套分析方法而能得到電廠管制單位的認可，也是同樣具有法律效應的。
國際管線完整性研究計畫( International Piping Integrity Research Group, IPIRG ) [ 9, 10, 11, 12]則考慮管路承受實際動態負載(如地震、振動)時管系的破裂行為，以驗證傳統齊頭式斷管( Double-ended Guillotine Break, DEGB )破壞準則的必要性，研究表明過去防止管線揮打(pipe whipping)而設立過多的固定支承設計是不必要和有害的，並將相關研究推廣至肘管、歧管等。此計畫是由美國核能管制委員會出資並集合世界核能先進國家投資Battle實驗室，由八個國家和地區組織起來成立的共同完成的計畫，進行管路系統破壞有關實驗及有限元素分析，並發展出一套可信、簡單的工程評估法，逐步建立核能管路系統安全評估的規範。第一期歷時4年(1987-1991)，第二期歷時5年(1991-1996)，由於經費限制，未能開展第三期的計畫。
在第一期與第二期IPIRG 計畫之間，又同時執行短裂縫計畫[13, l4,15]，研究的裂縫型態包含管路穿壁裂縫( Through-Wall Crack )與表面裂縫( Surface Crack )。這些計畫對建立管路先漏後破破壞評估準則以及對運轉中電廠管路缺陷檢測與安全評估都有所貢獻。美國短裂縫研究計畫是在美國NRC的要求和資助下，從1990年3月開始進行了，管線和管線焊接接縫中的短裂縫研究計畫，其主要目的是驗證和改進含圓周向短裂縫大直徑管線的評估方法，改變ASME Section III中，對管線缺陷評估方式以設計應力為主的規則。這裏重點強調的是在該研究計畫中，Battelle實驗室將國際上已發表和未發表的管線斷裂試驗資料進行了整理，建立了材料資料庫(PIFRAC)與圓周向裂縫管線資料庫(CIRCUMCK.WK1)，包括了220個軸向和700多個周向壓力管線斷裂試驗的原始資料和試驗結果，對壓力管線缺陷安全評定技術的研究具有十分重要的意義。
BINP ( Battelle Integrity of Nuclear Piping, BINP )[16]計畫為國際管路完整性合作研究群計畫( IPIRG-I, II )的後續計畫，主要目的在精進管路先漏後破技術與運轉中管路缺陷評估( In-service Flaw Evaluation )等相關技術。重點工作之一是建立廠用系統( Balance-of-Plant, BOP )管路及Class II, III 管路的缺陷評估準則。由於廠用系統管路及Class II, III 管路的操作壓力通常小於Class I 管路，因而有較大的R/t 比，其缺陷評估準則必然不同於ASME 法規為Class I 管路(R/t<15)所訂定的規範。為了建立運轉中管路缺陷評估準則，計畫中設計一系列測試分析( Round-Robin #2 )問題，針對不同R/t 比之含圓周向表面裂縫直管，請各會員國自行選擇工具與分析方法計算裂管在不同彎曲力矩負荷下之J 積分值，並於技術諮詢委員會議討論比對結果，希望能確立一套準確評估工具，進而協助建立BOP 管路及Class II, III管路的缺陷評估準則。為提昇國內技術能力，我國由原子能委員會、台電公司與核能研究所共同出資陸續參與IPIRG I、II 以及BINP 計畫。配合BINP 計畫要求，我國已經完成Round-Robin #2 所有問題之分析工作，本文即針對分析流程及結果作一介紹，並與其他會員國計算值作比較。
針對高勁度、低強度的延性材料(如不銹鋼)，J-積分是一種非常有效的分析方法，提供裂縫管線的破壞行為一種準確的評估方法。過去有很多關於穿壁裂縫直管的文獻，例如：Sanders (1982年, 1983年) [17, 18]基於殼理論，利用半解析法分別求解圓周向穿壁裂縫直管承受軸向拉力和彎矩的應力強度因子( stress intensity factor )。Paris和Tada法(1983年)[19]是Paris和Tada針對受純彎矩的直管，利用線彈性( linear elastic )和完全塑性載重( fully plastic loading )理論組成的：在彈性解的部份，採用了Irwin(1957年)[20, 21]裂縫有效尺寸的修正方式，有效裂縫長度由真實裂縫長度，再加上塑性區修正半徑；而在塑性解的部份，建立在完全塑性理論。因為塑性區修正半徑並沒有一個精確理論基礎，它的塑性區往往會大於實際的範圍，故在工程上只是一種近似法。LBB.NRC法(Klecker (1986年)) [22]的發展源自於Paris和Tada法，由Klecker (1986年)提出，不同點在於，將塑性材料性質由完全塑性理論改成應變硬化理論，不僅可以分析受純彎矩作用的案例，亦可用以評估受軸向力和彎矩共同作用之案例，與Paris和Tada(1983年)相同的特性，就是缺少明確的理論背景，皆為許多案例計算結果廻歸所得的經驗公式。LBB.GE( 亦稱LBB.ENG1 )法[23, 24, 25]則是1987年Brust參考GE/EPRI法 [26]中J積分公式；在塑性解中，若為長裂縫(裂縫角度大於30度)，則忽略塑性轉角，若短裂縫(裂縫角度小於30度)，則使用了LBB.NRC法中所定義的塑性轉角。Brust對分析模型作了修正後提出LBB.ENG2法[23, 27, 28, 29]，Brust認為管線中缺陷的存在會薄化管線斷面，故將該模型將薄化區段的厚度假設成一有效厚度，而非原來的管厚。LBB.GE法和LBB.ENG2法公式推導的依據，皆是建立在4點彎矩(four point bending) 模型上。Kumar和German (1988年) [30]應用GE/EPRI法來估算J-積分和COD值，報告中除了各別載重為軸向力和彎矩外，亦有等比例的組合載重。Zahoor [31]亦利用Sanders的解法，參考其封閉解(closed form)的形式，建立了J-積分的手冊，提供各種案例一種簡易的J-積分法；彈塑性J-積分由考慮有效裂縫長度的線彈性解與考慮非線性Ramberg–Osgood材料性質的完全塑性解所組合。
Kim等人(2001年) [32]利用強化參考應力法( enhance reference stress, ERS )計算J-積分和裂縫開口位移量( crack opening displacement, COD )，研究中針對分別承受軸向力和彎矩的圓周向穿壁裂縫直管，探討不同材料性質及幾何條件下的J-積分和COD。強化參考應力法[32]主要是藉由J積分的過程中，提供一參考應力，此參考應力能有效降低GE/EPRI法中塑性影響函數對J積分的影響程度；塑性影響函數取決於結構元件的幾何形狀與Ramberg-Osgood材料性質中的參數。強化參考應力法中的材料性質不經由曲線配適法( curve fitting )，直接使用真實的拉力實驗的數據；若實驗數據非常有限，則直接取極限塑性載重來定義一相對應的參考應力[33, 34]；反之，則是採用全段應力應變曲線來當材料性質。
不論劣化直管是具有何種的裂縫型態，承受何種的負荷類型，基本上無法以解析解方式得到裂縫J積分值，一般皆利用如有限元素法等數值方法計算裂縫J-積分值，再將計算結果整理成簡易數學公式方便工程師使用。例如，Zahoor [31]手冊中的案例，均是利用有限元素法發展出各類型劣化管路的J積分計算公式。但是這些公式通常僅適用於某些尺寸或是材料性質的管線，其他尺寸或是材料性質管線之J積分值則須利用現有資料內插得到，當現有資訊有限，內插J-積分值之準確度則有待商榷。有鑑於此，本研究亦針對圓周向穿壁裂縫直管，以商業軟體「ABAQUS」[35]建立有限元素模型，並架構在塑性變形理論( deformation theory of plasticity )的基礎上，而材料性質則是採用Ramber-Osgood法的應力應變曲線，探討各參數對J-積分的影響。
貳、有限元素驗證
一、 材料性質
首先，為了要驗證有限元素模型的正確性，本研究須與Kumar和German [30] ( ENPRI-NP-5596 )文獻比較。不同材料特性會影響J-積分計算結果，主要與材料應力-應變性質有關。然而，GE/EPRI法以Ramberg-Osgood關係式為材料曲線︰
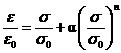(1)
式中，σ0參考應力，通常以材料的降伏應力(yield stress)作為參考應力；ε0=σ0/Ε為對應之參考應變，Ε為材料彈性模數；α與n則為材料Ramberg-Osgood參數，n又稱為材料的應變硬化指數( strain hardening exponent )。GE/EPRI法的J-積分公式是將許多案例以有限元素計算出結果，再以curve fitting方式迥歸出來的簡單公式，故並不是任意材料、任意幾何形狀的管線都適用(例如，Kumar和German [30]只列出裂縫角度為22.5°、45°、90°、180°，α=1，n=1,2,3,5,7等案例之參數。)。若查詢發現所用之案例並不在其中，則必須經由內、外插法得到公式中的相關參數，自然而然，精確度就會降低。本研究與Kumar和German [30]驗證時，所用的材料性質為α=1，n=2,5。在案例分析時，所用的材料則是核能電廠使用較多的不銹鋼之一型「SA312 TP316」，其材料性質如圖1所示，本研究採用曲線B (α=5.76，n=4.11)。由於台灣自1986 年起由台電公司、原能會及核研所共組以半會員身分加入IPIRG-1 & 2及BINP，透過此管道取得相當多的核能電廠管路材料的拉伸及J-R試驗資料。
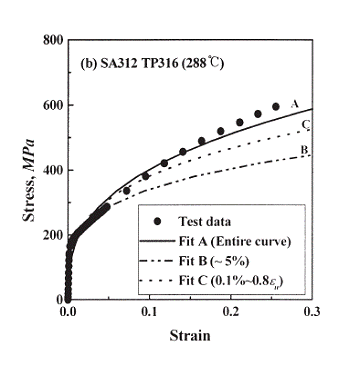
圖1 不銹鋼材料應力-應變曲線圖
二、幾何參數
圖2所示為本研究之圓周向穿壁裂縫直管示意圖：左圖為管子斷面，白色(2θ)部分為裂縫自由表面處，Ro為外徑，Ri為內徑，t為管厚，Rm為平均半徑為，2θ為裂縫角度，2a為半圓周長；右圖表示管子受軸向拉力和彎矩的情況。管路長度為管路外徑的五倍長，已可兼顧計算效率與精確度。
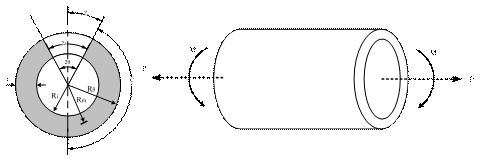
圖2 圓周向穿壁裂縫直管受軸向拉力和彎矩示意圖
三、有限元素模型
本研究使用有限元素軟體-「ABAQUS」建立管線模型，此模型共有957個元素，5338個節點。厚度方向有兩層網格(如圖3所示)，共有五個節點，最後的J-積分值取的是第一點、第三點、第五點加權後的平均值，如下
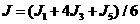(2)
其中，J1是管壁最內側節點的J-積分值，J3是管壁中間節點的J-積分值，J5是管壁最外側節點的J-積分值。模擬管線所使用的元素-「C3D20R」為三維等參數固體元素，每個元素有20個節點(如圖4所示)，採用減化積分點的高斯積分。由於本分析模型具對稱性，故只建立1/4 直管，並利用邊界條件模擬對稱行為。圖5中有符號之處即代表施加束制的邊界條件，斷面上其他沒有邊界條件符號之節點即為裂縫自由表面。圖6為裂縫前緣有限元素分割情形，網格以放射狀方式由裂縫尖端向外發展，此處元素分佈較密集，以得到詳細應力結果，進而正確計算J 積分值。在外力施加方式分成二種：一將軸向拉力轉換成均勻拉力作用在管路兩端的斷面上(如圖3所示)，另一則是將管路兩端的斷面視為剛性面，於中心點施加一彎矩(如圖7所示)，圖中向上的箭頭即代表彎矩的向量。由此可以看出不論是受軸向拉力，或是彎矩，裂縫處都是呈現開放的模式，而非擠壓裂縫表面。網格分割的規則性與粗細度亦可能影響計算結果及效率。本分析在管路軸向及周向的網格皆採均佈分割(如圖2、圖5、圖6、圖7)，周向部份為每5°分割一網格，軸向部份則將管路分為兩個區域，前區每一網格長度為(外徑/10)，共12 個網格，約佔管長1/4，其餘部份網格長度為(外徑/5)。
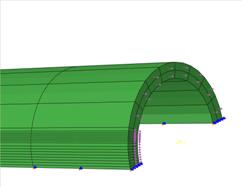
圖3 受軸向拉力作用之3D有限元素網格(1/4模型態)
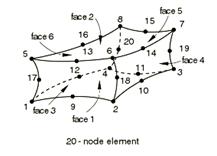圖4 20個節點的元素
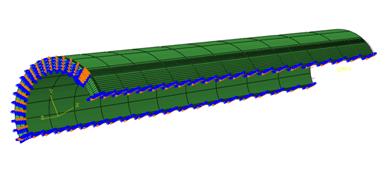
圖5 3D有限元素邊界條件
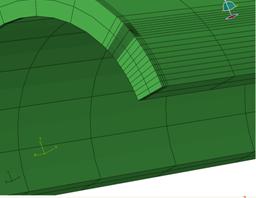
圖6 3D有限元素裂縫前緣網格
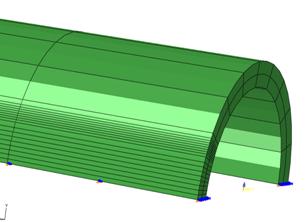
圖7 受彎矩作用之3D有限元素網格(1/4模型態)
四、驗證結果
一般作用於管子重要斷面之負荷大小在管線系統設計階段即經由應力分析得到，分析考慮之負荷包含內壓、自重、熱膨脹、地震、以及安全閥開啟與冷卻水喪失意外等所產生之動態負荷，這些負荷對於管路斷面影響通常以一軸向力P 與彎曲力矩M 代表。本研究分別考慮劣化直管在軸向拉力與彎曲力矩作用下之J-積分值。此小節將比較本研究之分析模型與Kumar和German [30]所評估出來的J-積分值，本研究之有限元素彈塑性分析是以「塑性變形」理論為基礎，而Kumar和German [30]則是以「塑流」理論。兩者的材料性質都是使用Ramberg-Osgood法則，其他的材料與幾何性質為：E=3*103ksi，σ0=50ksi，α=1，n=2,5，ν=0.3，外半徑Ro=2.1in，內半徑Ri=1.9in，管厚t=0.2in，平均半徑與厚度比為Rm/t=10 ，裂縫角度2θ=90°,180°。
GE/EPRI法中Kumar和German [30]發展出彈塑性J-積分的公式，基本上將J-積分值分為彈性與塑性兩部分個別計算再相加而得到。含圓周向裂縫直管在彎曲力矩作用下J-積分的公式：
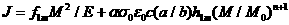(3)
而針對在軸向拉力作用下之J 積分值：
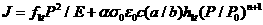(4)
其中，M 為作用於龜裂斷面之彎矩負荷；E為材料彈性係數 ；σ0，ε0，α，n為材料Ramberg-Osgood 參數；其他參數之定義與計算方法如以下所示:
(1) a =Rm θ ，a為裂縫圓周長度的一半，R 與θ之定義參考圖2。
(2) b =Rm π；
(3) c =Rm (π-θ)；
(4) 
，
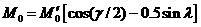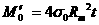，M'與M0分別是完整直管斷面與含裂縫斷面所能承受之極限力矩。
(5) 
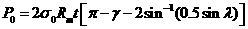為含裂縫斷面所能承受之極限拉力。
(6) 
、
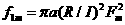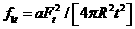，之中 I=π(Ro4-Ri4)/4 為直管斷面慣性力矩，Ro=Rm+t/2，Ri=Rm-t/2；Fm和Ft為參數(可查表得之)，它的值視a/b 以及R/t 值而定。
(6) h1m、h1t為參數(可查表得之)，它的值視a/b 、R/t 以及n 值而定。
Kumar和German [30]針對R/t =5、10、20，a/b=1/16、1/8、1/4、1/2，n=1、2、3、5、7，將Fm、Ft、h1m、h1t以表列方式表示，方便大家使用。但是對於具有不同尺寸或是材料管子，則必須以內、外插方式得到，或是使用數值方法進行分析。
針對受軸向拉力的案例，圖8中左圖為短裂縫(22.5°)，右圖為長裂縫(90°)，線條的部分是Kumar和German 之J-積分公式，而點的部分則是有限元素法。由圖8中可以發現不論是短、長裂縫，有限元素法與Kumar和German的結果非常接近。同理，圖9針對受彎矩的案例，驗證的結果亦與Kumar和German的一致。由此可見，本研究所建立的分析模型非常精確。
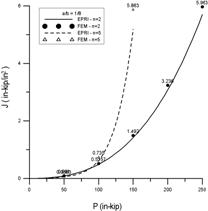
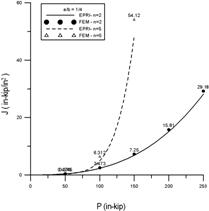
圖8 受軸向拉力作用下，有限元素法與GE/EPRI法之J-積分值比較
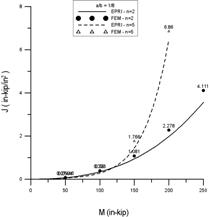
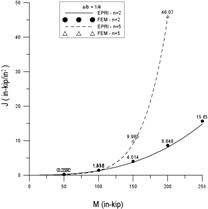
圖9 受彎矩作用下，有限元素法與GE/EPRI法之J-積分值比較
本研究所用之裂縫J-積分值以管厚斷面上中下三個節點加權之後，再平均的方式(如式2所示)。J-積分公式在數學上是一封閉曲線的避點積分，J-積分值與積分路徑無關。在數值分析上理應如此，但由於數值積分會造成誤差，愈接近裂縫尖端處( crack tip )，應力或應變之變化愈大，有限元素的網格( mesh )就要愈密集，才能符合「與積分路徑無關」的理論。當然，網格可以一直增加到滿足這現象，但成本上的花費是不是能符合投資報酬，才是更重要的關鍵。故以經濟為考量的前題下，本研究不選擇最接近裂縫端點的路徑，而是從裂縫尖端起取五條路徑，表一中顯示第一圈與第五圈J-積分值的平均誤差僅約2.2%。基於統一起見，以下章節敘述之J-積分值皆為第五圈J-積分值的平均。
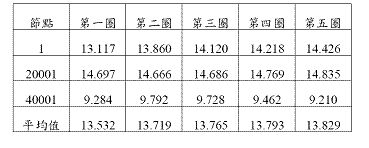
表一、裂縫前緣節點J 值計算結果(單位:1000 lbf/in)
參、案例分析
不銹鋼是由鐵、鉻、鎳及其他不同元素所組成的合金，鐵是主要成分元素，鉻、鎳是主要的合金元素。一般而言，若鉻含量不足，則不銹鋼表面將無法形成氧化鉻保護膜，而失去防銹的功能。若鉻的含量足夠，在常溫大氣中，是不會生銹的。然而，不同元素在不同比例下所合成的不銹鋼，將產生不同的材料強度。材料強度關係到管線是否斷裂的主因之一，故在案例分析中，先針對材料性質中的應變硬化指數(n)對J-積分值的影響，加以探討。材料進入塑性之後，若α不變，應變硬化指數愈大，則材料的極限強度愈小。從圖8和圖9可以看出應變硬化指數對裂縫的影響：當n愈大，材料強度愈小，J-積分值愈大。在物理的層面上，J-積分可代表一「裂縫驅動力」，是一種廣義的裂縫端點力。J-積分值愈大，表示裂縫驅動力愈大，裂縫就愈容易擴展；反過來說，如果要阻止裂縫擴展，就要付出更大的阻力。因此，如圖8和圖9所示，在其他參數固定的情況下，當n愈大，含裂縫的管線就愈脆弱。
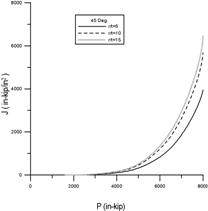
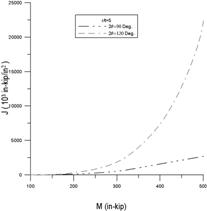
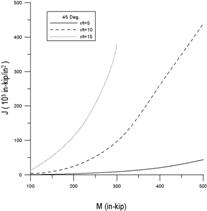
圖10和圖13中，材料性質為核能電廠管線經常使用的不銹鋼(SA312 TP316, 288℃)：E=190GPa，σ0=165MPa，α=4.72，n=3.39，ν=0.3；而幾何性質為：管厚t=0.04m，平均半徑與厚度比分別為Rm/t=5,10,15，裂縫開裂角度2θ=30°,45°,60°,90°,120°。圖10為受軸向拉力作用下，不同裂縫大小(30, 45, 90, 180度)的J-積分值，從圖中發現，角度愈大的裂縫，其J-積分值愈大。換句話說，當裂縫愈大，能量釋放率愈大，裂縫就愈容易擴展。圖10(a) 裂縫角度為30度和45度之J-積分值明顯比圖10(b)90度和120度之J-積分值小了很多；圖10(a)的J-積分值最多約1,200(103in-kip/in2)左右，而圖10(b)卻是5,000(103in-kip/in2)左右。圖11為Rm/t=5,10,15時之J-積分值，經由比較可以得知管線厚度對J-積分值影響，在相同裂縫下，當管線愈薄時，強度愈弱，J-積分值愈大，裂縫愈容易擴展。圖12和圖13為受彎矩作用下，J-積分值的變化趨勢，但與圖10-11(受軸向拉力作用)卻有顯著的不同點：(1) 圖12(a)和(b) 長短裂縫的J-積分值差異更大了。短裂縫的J-積分值大約在1,000(103in-kip/in2)以內，而長裂縫卻高達25,000(103in-kip/in2)，由此可知，當管線受到彎矩作用時，J-積分值對於裂縫大小是很敏感的，特別是長的裂縫。(2) 圖13在探討管線厚度對J-積分值的影響，由圖13發現J-積分值差異遠比在受軸向拉力作用下的案例更大。由此可見，在面對彎矩作用時，應注意管線厚度的變化，特別是運轉時間長久的管路，常常會因侵蝕或腐蝕而造成管線薄化，管線一旦薄化，其強度勢必減弱。
(a)
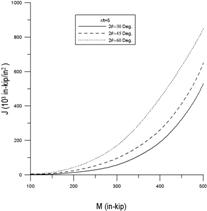(b)
圖10 受軸向拉力作用下，不同裂縫大小之J-積分值：
(a) 30度和45度； (b) 90度和120度。
(a)
圖11 受軸向拉力作用下，裂縫角度45度在不同厚度(r/t=5, 10, 15)之J-積分值
(a)
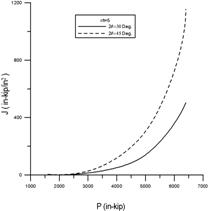(b)
圖12 受彎作用下，不同裂縫角度之J-積分值：
(a) 30度、45和60度； (b) 90度和120度。
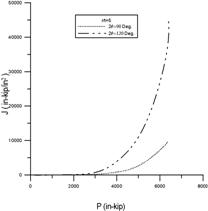
圖13 受彎作用下，裂縫角度45度在不同厚度(r/t=5, 10, 15)之J-積分值
肆、結論
壓力管線斷裂一直是造成核能電廠嚴重事故的主因之一，世界先進國家紛紛對壓力管線進行LBB(先漏後破)的研究，並提出相對應的判斷準則。J-積分便是其中一種用以判別裂縫是否擴展的物理量。因此，本研究主要針對含圓周向穿壁裂縫直管，分別承受軸向拉力和彎矩作用下，建立彈塑性有限元素模型，計算出J-積分值，並探討材料性質與幾何參數改變對J-積分值的影響。綜觀全文，歸納出下列幾點：
(1) 材料進入塑性之後，若α不變，應變硬化指數愈大，則材料的極限強度愈小，J-積分值愈大，則「裂縫驅動力」愈大。
(2) 當裂縫長度增加，無論外力載重為何，都將削弱管線強度，增加能量的釋放率，裂縫就愈容易擴展。這種現象在長裂縫明顯大於短裂縫。
(3) 當裂縫大小相同，且管線愈薄時，強度愈弱，J-積分值愈大，裂縫愈容易擴展。特別是受彎矩作用，薄化對管線強度減弱更加明顯。
(4) 目前，對於含圓周向穿壁裂縫直管的J-積分並無文獻提出解析解(analytic solution)，本研究提出的有限元素數值解(numerical solution)，對於管線評估上，提供一迅速且精確的參考依據。
伍、參考文獻
1. ASME, 1995, Boiler and Pressure Vessel Code.
2. NUREG-0313, 1977, Technical Report on Material Selection and Processing Guidelines for BWR Coolant Pressure Boundary Piping, USNRC, Washington, DC, USA.
3. NUREG-0313, Rev. 1, 1980, Technical Report on Material Selection and Processing Guidelines for BWR Coolant Pressure Boundary Piping, USNRC, Washington, DC, USA.
4. NUREG-0313, Rev. 2, 1980, Technical Report on Material Selection and Processing Guidelines for BWR Coolant Pressure Boundary Piping, USNRC, Washington, DC, USA.
5. Wilkowski, G. M., Kanninen, M. F., Marschall, C. W., Pan, J., Popelar, C., Broek, D., Ahmad, J., and Gilbert, R., 1983, “Summary of NRC Phase I Degraded Piping Program – Instability Analyses and Review of Experimental Programs to Evaluate J/T Instability Predictions,” Circumferential cracks in pressure vessels and piping: presented at the 4th National Congress on Pressure Vessel and Piping Technology, ASME, Portland, Oregon, USA.
6. Wilkowski, G. M., Ahmad, J., Barnes, C. R., Brust, F., Ghadiali, N., Guerrieri, D., Jones, D., Kramer, G., Landow, M., Marschall, C. W., Olson, R., Papaspyropoulos, V., Pasupathi, V., Rosenfeld, M. , Scott, P., and Vieth, P., March 1984 - January 1989, Degraded Piping Program – Phase II , NUREG/CR-4082, v1-8.
7. ASME XI IWB-3640 and Appendix C[S] , l986, “Flaw Evaluation Procedures and Acceptance Criterion for Austenic Piping”, ASME, New York.
8. ASME XI IWB-3650 and Appendix H[S] ,1992 , “Evaluation Procedures and Acceptance Criterion for Ferritic piping”, ASME, New York.
9. Schmidt, R. A., Wilkowski, G.. M., and Mayfield, M., Aug. 1991, “The International Piping Integrity Research Group (IPIRG) Program – An Overview”, SMIRT-11 Proceedings, Paper G23/1.
10. NUREG/CR-6233, June 1997, International Piping Integrity Research Group (IPIRG) Program, BMI-2177, v4, USNRC, Washington, DC, USA.
11. Hopper, A., Wilkowski, G.. M., Scott, P., Olson, R., Rudland, D., Kilinski, T., Mohan, R., Ghadiali, N., and Paul, D., March 1997, The Second International Piping Integrity Research Group (IPIRG-2) Program- Final Report, NUREG/CR-6452, BMI-2195, USNRC, Washington, DC, USA.
12. NUREG/CR-6765, May 2002, Development of Technical Basis for Leak-Before-Break Evaluation Procedures, USNRC, Washington, DC, USA.
13. Wilkowski, G. M., Ahmad, J., Barnes, C.R., Brust, F., Ghadiali, N., Guerrieri, D., Jones, D., Kramer, G., Landow, M., Marschall, C. W., Olson, R., Papaspyropoulos, V., Pasupathi, V., Rosenfeld, M. , Scott, P., and Vieth, P., 1991-1994, Short Cracks in Piping and Piping Welds, NUREG/CR-4599, v1-3, USNRC, Washington, DC, USA.
14. Stoppler, W., Sturm, D., Scott, P., and Wilkowski, G. M., Oct.1992, “Analysis of the Failure Behavior of Longitudinally Flawed Pipes and Vessels [R] ,” 18th MPA Seminar, v1, pp.28-1 to 28-5.
15. Scott, P., Wilkowski, G., Sturm, D., and Stoppler, W., 1994, “Development of a Database of Pipe Fracture Experiments,” Nuclear Engineering and Design, v151, n2-3, pp.359-371.
16. Scott, P., Olson, R., Bockbrader, J., Wilson, M., Gruen, B., Morbitzer, R., Yang, Y., Williams, C., Brust, F., Fredette, L., and Ghadiali, N., 2005, The Battelle Integrity of Nuclear Piping (BINP) Program Final Report, NUREG/CR-6837, v1-2, USNRC, Washington, DC, USA.
17. Sanders, J. L., 1982, “Circumferential Through-Cracks in Cylindrical Shells Under Tension,” ASME, Journal of Applied Mechanics, v49, pp. 103-107.
18. Sanders, J. L., 1983, “Circumferential Through-Cracks in Cylindrical Shells Under Combined Bending and Tension,” ASME, Journal of Applied Mechanics, v50, pp. 221.
19. Paris, P. C., and Tada, H., 1983, The Application of Fracture Proof Design Methods Using Tearing Instability Theory to Nuclear Piping Postulating Circumferential Through-Wall Cracks, NUREG/CR-3464, USNRC, Washington, DC, USA.
20. Irwin, G. R., 1957, “Analysis of Stresses and Strains Near the End of a Crack Traversing a plate,” ASME, Journal of Applied Mechanics, v24, pp. 361-364.
21. Irwin, G. R., 1961, “Plastic Zone Near a Crack and Fracture Toughness,” 7th Sagamore Research Conference Proceedings, v4.
22. Klecker, R., Brust, F., and Wilkowski, G. M., , 1986, NRC leak-before-break(LBB.NRC) Analysis Method for Circumferentially Through-Wall Cracked Pipes Under Axial Plus Bending Loads, NUREG/CR-4572, USNRC, Washington, DC, USA.
23. Brust, F., 1987, Approximate Methods for Fracture Analysis of Through-Wall Cracked Pipes, NUREG/CR-6235, USNRC, Washington, DC, USA.
24. Gilles, P., and Brust, F. W., 1991, “Approximate Fracture Method for Pipes-Part I: Theory,” Nuclear Engineering and Design, v127, pp1-17.
25. Gilles, P., Chao, K. S., and Brust, F. W., 1991, “Approximate Fracture Method for Pipes-Part II: Applications,” Nuclear Engineering and Design, v127, pp.19-31.
26. Kumar, V., German, M. D., Wilkening, W. W., Andrews, W. R., deLorenzi, H. G., and Mowbray, D. F., August 1984, Advances in Elastic-Plastic Analysis, EPRI NP-3607.
27. Rahman, S., Brust, F., Nakagaki, M., and Gilles, P., 1991, “An Approximate Method for Estimating Energy Release Rates of Through-Wall Cracked Pipe Weldments,” Fatigue Fracture and Risk, PVP 215, San Diego, California.
28. Rahman, S., and Brust, F., 1992, “An Estimation Method for Evaluating Energy Release Rates of Circumferential Through-Wall Cracked Pipe Welds,” Engineering Fracture Mechanics, v43, n3, pp.417-430.
29. Gilles, P., Brust, F. W., 1994, “Approximate Methods for Fracture Analysis of Tubular Members Subjected to Combined Tensile and Bending loads,” Journal of Offshore Mechanics Artic Engineering, v116, n4, pp. 221-227.
30. Kumar, V., and German, M. D., 1988, Elastic-Plastic Fracture Analysis of Through-Wall and Surface Flaw in Cylinders, EPRI NP-5596.
31. Zahoor, A., Oct. 1990, Ductile Fracture Handbook, v2 & v3, Novetech Corp., Gaithersburg, MD, USA.
32. Kim, Y. J., Huh, N., and Kim, Y. J., 2001, “Enhanced Reference Stress-Based J and Crack Opening Displacement Estimation Method for Leak-Before-Break Analysis and Comparison with GE/EPRI Method,” Fatigue and Fracture of Engineering Materials and Structures, v24, n4, pp. 243-254.
33. Ainsworth, R. A. , 1984, “The Assessment of Defects in Structures of Strain Hardening Materials,” Engineering Fracture Mechanics, v19, n4, pp 633–642.
34. R6: Assessment of the Integrity of Structures containing Defects, Revision 4, British Energy Generation Ltd, Gloucester, UK, 2001.
35. ABAQUS Version, 6.8-1, 2010, User’s Manual, Hibbitt, Karlsson and Socrensen, Inc., Pawtucket, RI, USA.
