朱 信 忠      童琮樟（核能研究所化工組）

摘  要

本研究以瑞典 KBS-3 之深層地質處置設計概念，搭配瑞典 Site-94 及芬蘭 TILA-99 之化學、傳輸與地質等參數數據，作為用過核子燃料最終處置之範例，進行處置場封閉後期人體輻射劑量率之機率式評估分析，而核種釋出率及人體輻射劑量率則分別以 INPAG-N 與 INPAG-F 電腦程式及芬蘭 WELL-97 模式進行分析，並以 Kolmogorov-Smirnov 統計測試法（KS-Test）探討機率式安全分析結果之收斂性議題。

在本研究範例中，分佈型參數共有 67 個，分佈型態分別為均一、對數均一、常態、及對數常態等分佈，並以拉丁超立體取樣法來對這些分佈型參數進行取樣，而機率式安全分析之運跑回合數則分別設定為 70、100、及 200 等三種不同情況，且在每一種情況下又各自獨立測試五次，總共得 15 道人體輻射劑量率峰值之 CCDF 曲線。

以 KS-Test 對這 15 道 CCDF 曲線進行測試之結果得知：在 67 個分佈型參數及拉丁超立體取樣法的情況下，即使低至 70 之運跑回合數亦可獲得穩定、可信、收斂的機率式安全評估結果。

關鍵字：放射性廢棄物、用過核子燃料、深層地質處置、功能與安全評估、機率式評估、Kolmogorov-Smirnov 統計測試法

 

一、前言

在核能發電技術已發展至安全無虞之年代裡，核能之永續應用與發展端賴放射性廢棄物（radioactive wastes）是否能安全地處理與永久處置。我國於民國七十五年起由台電公司結合核能研究所、工研院能資所（現已更名為能環所）、中央地調所及國內大學開始研究我國用過核子燃料(spent nuclear fuel，簡稱 SNF)最終處置（final disposal）相關問題與技術。核能發電廠之高放射性廢棄物(high-level radioactive wastes，包括 SNF)之最終處置方式，目前國際上一致公認最為可行、最為可靠者為採取多重障壁系統（multiple barriers system）的深層地質處置（deep geological disposal）概念^[1-8]，如圖1 所示。

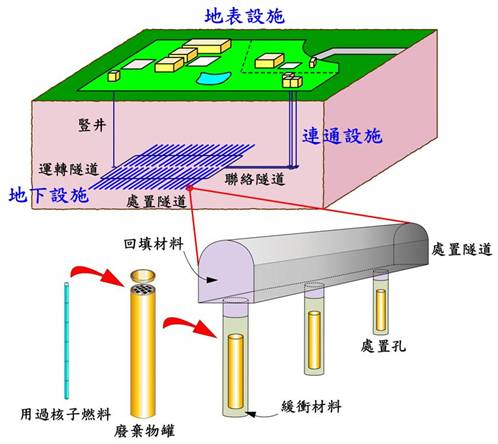
圖 1  深層地質處置多重障壁系統概念示意圖

圖1 顯示在多重障壁之深層地質處置場中，廢棄物罐（canister 或 container）內之放射性廢棄物必須通過層層之阻礙才能進入人類的生活圈。多重障壁系統包括工程障壁（engineered barrier）及天然障壁（natural barrier）；工程障壁包含廢棄物體（waste form）、廢棄物罐、緩衝層（buffer layer） 及回填層（backfilled layer）等，其主要功能係用來保護廢棄物罐，阻止、延緩地下水入侵處置孔（disposal pit），並降低廢棄物體中放射性核種（radionuclide，以下簡稱核種）之釋出率（release rate）。緩衝層主要材料為膨潤土(Bentonite)或膨潤土搭配少量之細砂或處置場址開挖物，回填層的材料一般則為膨潤土與細砂或膨潤土與處置場址開挖物之適量配比混合物。天然障壁則利用穩定之地質母岩的特點來保護工程障壁系統，並減緩核種遷移至人類生活環境(又稱生物圈，biosphere)，穩固的地質母岩除了提供工程障壁系統一個長期安定不受擾動的機械與化學環境及甚少地下水流動外，亦可吸附從工程障壁外釋出來之核種。深層地質處置場一般建造在地表下方約 300 至 1000 公尺間的穩定母岩中，其目的一方面係避免未來人類不當的入侵，另一方面則可防止或減低地表環境變化的影響。

核種在工程障壁中之遷移與釋出完全受到工程障壁及天然障壁之材質、化學、傳輸及地質特性，諸如廢棄物體溶解速率、化學元素溶解度（solubility）及吸附（sorption 或 distribution）係數、擴散（diffusion）係數、孔隙率(porosity)、材質密度、地下水流速、裂隙內寬（fracture aperture）、裂隙間距（fracture spacing）等等因素的影響，而這些參數在深層地質處置場中往往具有很大的區域變異性（variability）及不確定性（uncertainty），因此評估 SNF 深層地質處置場核種之釋出率，其所得之結果亦將具有很大的不確定性，故處置場之安全分析除了進行確定性（deterministic）之評估外，尚必須進行機率式（probabilistic）之評估，以瞭解核種釋出率之上、下限極值及機率分佈。本文作者曾以日本 H12 之設計概念^[5]作為研究對象，進行工程障壁核種釋出率之不確定性與參數敏感度分析（uncertainty and sensitivity analysis）研究^[9,10]。當參數之不確定性範圍縮小時，則核種釋出率評估結果之不確定性亦會隨之而降低，然而地質探勘與參數量測是件十分耗費人力、物力與時間之工程，為了經濟有效地運用有限之人物力與時間，一般作法為先探究那些對核種釋出率具有重大影響的參數，在行有餘力之下，接著再針對次要之參數進行探討，並依序類推至最不敏感之參數。

機率式評估建立在多重運跑評估方法上，也就是反覆地對系統進行分析，每次給予分佈型參數不同之數值，再將分析所得之結果進行整合，並以機率分佈的方式來呈現評估結果。既然必須進行多回合之分析，那麼在機率式評估方法上就出現了一個議題：到底需要反覆進行多少回合之分析才能得到穩定、可靠、收斂的機率式評估結果呢？又機率式評估結果之穩定、可靠、收斂與否又要如何判斷呢？為了探討這樣的議題，本文特地以以瑞典 KBS-3 之深層地質處置設計概念^[11]，搭配瑞典 Site-94^[1] 及芬蘭 TILA-99^[3] 之化學、傳輸與地質等參數數據，並設定其中 67 個參數為分佈型參數，作為標的研究範例，進行處置場封閉後期（post closure）人體輻射劑量率之機率式評估分析，分析工具則分別採用 INPAG-N 與 INPAG-F 電腦程式^[12-15]及芬蘭 WELL-97 模式^[16]，而運跑回合數則分別設定為 70、100 及 200 等三種不同情況，且每一種情況下又各自獨立運跑五次，因此總共獲得 15 道人體輻射劑量率峰值之 CCDF （complementary cumulative density function） 曲線，接著再利用 Kolmogorov-Smirnov 統計測試法^[17]（簡稱 KS-Test）來對這 15 道 CCDF 曲線進行交互比較分析，以探討多少回合之分析才可獲得穩定、可靠、收斂的機率式安全評估結果。

二、核種釋出率與人體劑量率評估

根據圖1所示之 SNF 深層地質處置概念，處置場中核種之釋出途徑（release pathway）可以概念簡化為如圖2所示。圖2顯示核種從廢棄物體中釋出並傳輸至人類生活環境之過程，被劃分為近場（near field）、遠場（far field）及生物圈等三個串接範疇來分別進行評估。

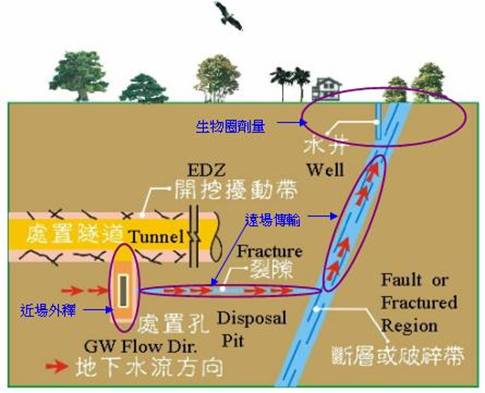
圖 2  核種釋出途徑概念

近場範疇涵蓋 SNF 廢棄物體、廢棄物罐、緩衝材層、EDZ（excavated disturbed zone 或 excavated damaged zone）及 EDZ 周圍未受擾動之母岩。當廢棄物罐接觸地下水並發生腐蝕破損時，其內之 SNF 廢棄物體將被地下水侵蝕而溶解，其中所含之核種因而開始藉著分子擴散、地下水平流（advection）及延散（dispersion）等機制向外遷移（migration）。核種從廢棄物體中之溶出受化學元素溶解度之限制，溶解之核種首先以分子擴散機制穿過腐蝕之廢棄物罐及緩衝材層，到達 EDZ 層後再以分子擴散、地下水平流及延散等機制繼續向 EDZ 周圍母岩遷移，核種在遷移過程中會受到介質吸附的阻礙。近場範疇分析核種遷移至 EDZ 周圍母岩之流率，稱為近場核種釋出率，本研究以 INPAG-N 程式^[12-14]來分析之。

遠場範疇涵蓋從 EDZ 周圍母岩至斷層（fault）或破碎帶（fractured region）間之固結地質母岩區間，遠場範疇分析核種遷移至斷層或破碎帶處之流率，稱為遠場核種釋出率，本研究以 INPAG-F 程式^[15]來分析之。

生物圈範疇則涵蓋從斷層或破碎帶、地表含水層（aquifer）、生物食物鏈，最後則到達人體造成人體之輻射劑量率（dose rate）之區間，本研究以芬蘭之 WELL-97 模式^[16]來分析生物圈範疇之人體輻射劑量率。WELL-97 是一個簡單的井水飲用情節，至於遠場釋出之放射性核種傳輸進入水井之流率則以一可調變之參數處理之。WELL-97 模式可以下列方程式表示：

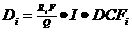 (1) 

其中 D_i 為因 i-核種而導致的人體輻射劑量率（Sv/yr）、R_i 為 i-核種在遠場之釋出率（Bq/yr）、F 為核種流入水井之分率（fraction，假設所有核種都同一數值）、Q 為水井之產水率（m³/yr）、I 為每人每年之飲水量（m³/yr）、DCF_i 為 i-核種之劑量轉換因子（dose conversion factor，單位為 Sv/Bq），而 DCF_i 係採用 ICRP-72 報告^[18] 之數據。

三、多重運跑架構

為了進行人體劑量率之機率式分析，吾人必須重複運跑 INPAG-N 及 INPAG-F 程式多次，每次對各個分佈型參數輸入不同的數值，再將所得結果彙整分析，以獲得各種不同標的之 CCDF 分佈結果，諸如劑量率峰值（peak dose rate）CCDF 圖、劑量率峰值發生時刻 CCDF 圖、或在某特定時刻之劑量率CCDF 圖等之機率分布結果^[9]。本研究擬重複運跑 INPAG-N及 INPAG-F 程式 70、100 及 200 次等三種不同情況，且每一種情況下又皆各自獨立運跑 5 次，本研究採用著名的拉丁超立體取樣（Latin hypercube sampling）技術^[19-24]，來分別製備 70、100 及 200 組之分佈型參數數值，以供 INPAG-N及 INPAG-F 程式運跑使用，多重運跑架構之執行方法與程序如圖3所示。

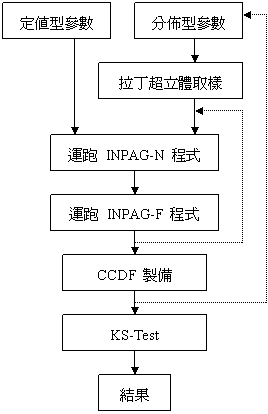
圖 3  多重運跑之執行方法與程序

四、KS-Test

KS-Test 被廣泛地應用來分析分佈型之數據組，以探討不同數據組間之差異，KS-Test 提供了一套無偏頗之定量化判斷準則（criterion）^[17]。KS-Test 不需對樣本數據組之分佈做任何假設，它對樣本數據組之 CDF （cumulative density function）曲線的形狀及位置敏感，只在乎數據組間的相對分佈，而與 X-軸的座標尺規無關。KS-Test 主要係根據 Kolmogorov 分佈函數及理論：

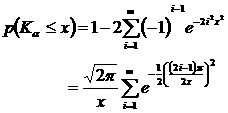(2)

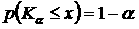(3)

其中，α 為重要度（significance level），而（1-α）則稱為信心度（confidence level）。

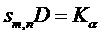(4)

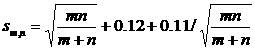(5)

其中，D 為兩道 CDF 分佈曲線之最大垂直距離，而 m 與 n 則分別為建構該兩道 CDF 曲線之樣本數目。D 值之計算方法如圖4 所示，其中該兩道階梯式曲線即是 CDF 分佈曲線，圖中之紅色垂直線段就是其最大垂直距離，該垂直距離不受 X-軸之的座標尺規的影響。

KS-Test 之應用方法為利用式(4) 與式(5) 計算出兩道 CDF 間之 S_m,nD 數值，再利用式(2) 與式(3) 計算出 α 數值，再根據 α 數值推論該兩道 CDF 曲線係相同或相異。Kolmogorov 的理論指出：若任何兩組數據組均係取自同一來源時，則其 CDF 分佈曲線間之 S_m,nD 值會符合式(2) 所示之關係（即 hypothesis test 中之 Null hypothesis）；若 S_m,nD 值超出式(2) 的預測之外或落入α 值內（一般設定 α=0.05，其對應之S_m,nD 值訂為 S_m,nD_α=0.05，也就是 S_m,nD > S_m,nD_α=0.05 之情況），則表示該兩組數據組係取自不同的來源（即 hypothesis test 中之 Alternative），有關 KS-Test 之理論與實際應用請參考相關文獻^[17]。

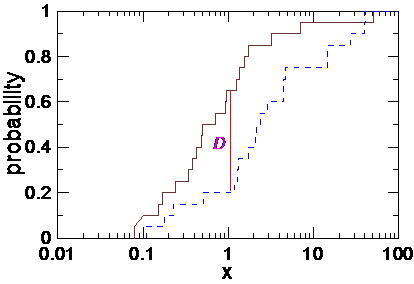
圖 4  KS-Test 之 D 值範例

五、參數數值

運跑 INPAG-N 及 INPAG-F 程式所需之參數相當多^[9,10,12-15]，所需參數之多寡又依所欲評估之核種數目而定，所評估之核種數目越多則所需之參數數目也越多，主要是核種化學特性參數，如溶解度及吸附係數等。本研究總共納入 37 個核種進行評估，包括活化與分裂產物（activation and fission products）及超鈾系（transuranic，簡稱 TRU）衰變鏈 4N、4N+1、4N+2、及 4N+3等，超鈾系衰變鏈成員如下所示：

4N：Pu-240àU-236àTh-232

4N+1：Cm-245àPu-241àAm-241àNp-237àU-233àTh-229

4N+2：Cm-246àPu-242àPu-238àU-238àU-234àTh-230àRa-226

4N+3：Am-243àPu-239àU-235àPa-231

該 37 個核種之半衰期（half-life）及初始存量（inventory）如表一所示，表一中最末欄為核種存量之瞬釋分率（instant release fraction，簡稱 IRF），SNF 的核種存量一般被粗分為兩類^[3]，分別為：存在於燃料丸表面與晶格邊界者，及存在於氧化物金屬基質（matrix）中者；核種存在於前者的分率稱為 IRF，IRF 核種與基質核種的溶解方式不同^[3]。

表一  核種初始存量表

表二所列者為本研究範例之工程障壁幾何相關設計參數及數值，其中廢棄物罐之壽命訂為十萬年，而廢棄物罐腐蝕後之密度設定為 0.0 者，則表示廢棄物罐腐蝕後完全沒剩餘物。表二之參數屬定值型參數，在不同運跑回合中其數值皆相同、固定不變動。

表二  工程障壁之幾何設計參數

工程障壁與母岩之材料特性及生物圈傳輸參數如表三所示，表三中含定值型與分佈型兩種參數，其中之分佈型參數在每個運跑回合其數值皆不同。表中之 U(a,b) 者為均一分佈（uniform distribution）、a 為下限值、b 為上限值，LU(a,b) 者為對數均一分佈（log-uniform distribution），N(m,s) 者為常態分佈（normal distribution）、m 為平均值、s 為標準差，LN(h,n) 者為對數常態分佈（log-normal distribution）、h 為對數平均值、n 為對數標準差。對於常態及對數常態分佈參數之取樣技巧可參考相關文獻^[25]，而有關均一與對數均一分佈之設定相當討論則可參考相關文獻^[26]。

表三  工程障壁與母岩之材料特定參數

化學元素之溶解度限值及其在緩衝材與母岩中之吸附係數如表四所列，其中之 1E6 代表數值1.0x10⁶，而 1E-3 則代表數值1.0x10^-3，餘者類推，表四中之上、下限值係根據 Site-94^[1] 及 TILA-99^[3] 而訂定。

表四  化學元素之溶解度及吸附係數

化學元素名稱	溶解度 (mol/m3)	緩衝材吸附係數(m3/kg)	母岩吸附係數(m3/kg)
C	1E6	LU(0,0.01)	1E-3
Cl	1E6	0	LU(0,1E-4)
Ni	LU(0.1,1E6)	LU(0.1,1)	LU(0.02,0.5)
Se	LU(3E-6,1E-3)	LU(0.003,0.01)	LU(5E-4,0.01)
Sr	LU(1E-3,3.0)	LU(0.01,0.2)	LU(2E-4,0.01)
Zr	LU(6E-7,1E-3)	LU(1,2)	LU(0.4,4)
Nb	LU(1E-5,1.0)	LU(0.2,1)	LU(0.1,2)
Tc	LU(8E-6,5E-5)	LU(0.05,0.1)	LU(0.01,1)
Pd	LU(1E-6,1E-3)	LU(0.01,1)	LU(0.01,0.5)
Sn	LU(4E-6,5E-3)	LU(0.2,3)	LU(1E-3,0.5)
I	1E6	LU(0,1E-3)	LU(0,1E-3)
Cs	1E6	LU(0.01,1)	LU(0.04,0.1)
Sm	LU(2E-4,1E-2)	1	LU(0.04,0.5)
Pu	LU(1E-7,5E-4)	LU(3,5)	LU(2,5)
U	LU(8E-6,1E-2)	LU(0.5,5)	LU(1,5)
Th	LU(1E-6,5E-3)	LU(1,5)	LU(0.5,5)
Cm	LU(9E-7,2E-4)	LU(2,5)	LU(0.5,5)
Am	LU(7E-6,5E-4)	LU(2,5)	LU(0.5,5)
Np	LU(2E-6,1E-4)	LU(1,5)	LU(0.5,5)
Ra	LU(1E-9,0.1)	LU(0.01,0.5)	LU(0.02,0.5)
Pa	LU(1E-5,3E-4)	LU(0.2,1)	LU(0.2,1)

六、結果與討論

6.1  劑量率之不確定性

根據圖3 所示之多重運跑的執行方法與程序來運跑 INPAG-N、INPAG-F、及式(1)，當取樣數目為 70時，電腦程式必須串接反覆運跑 70 次，若又在此取樣數目下獨立測試五次時，則電腦程式必須串接反覆運跑 350（5x70）次。因此在獨立測試五次取樣數目分別為 70、100、及 200下，電腦程式必須串接反覆運跑總共 1,850 次（5x70 + 5x100 + 5x200）。每一次電腦程式之串接運跑可以得到各個核種所導致之人體輻射劑量率隨時間變化之情形如圖 5 所示，圖中縱座標之單位為 Sv/yr，橫座標之單位為年（yr），圖中除了顯示各個核種者外（各種圖示），亦顯示人體總輻射劑量率隨時間變化之情形（紅色曲線）。圖 5 之結果顯示總劑量率峰值（peak dose rate）為 2.7E-8 Sv/yr，其發生時刻在 5.3E5 年。對於圖 5 之範例而言，最關鍵性之核種為 Th-229。

 

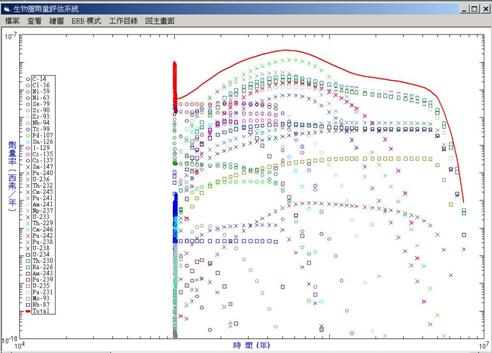
圖 5  各個核種造成人體輻射劑量率隨時間變化之情形

由於每回合之電腦程式串接運跑可得到一道人體總輻射劑量率隨時間變化曲線，當取樣數目為 100 時，可得人體總輻射劑量率曲線之可能情形如圖 6 所示，其中之灰色曲線共 100 道係程式運跑 100 次時，每次所得的人體總輻射劑量率。在圖中灰色曲線帶最下方之綠色曲線為第 5 百分比(percentile)位置(所謂第 5 百分比就是將 100 組數值從小到大依序排列後之第 5 個數值)、最上方之藍色曲線為第 95 百分比位置、上方下來第二道紅色曲線為平均值之位置、而上方下來第三道紫色曲線為第 50 百分比位置。圖 6 之結果顯示因參數數值變化導致人體總輻射劑量率隨時間變化之關係曲線出現了很大的不確定性，而且第 50 百分比曲線並不一定會與平均值曲線相吻合。灰色曲線帶愈寬代表評估結果之不確定性愈大，其寬窄由各參數數值之不確定性程度而決定。

 

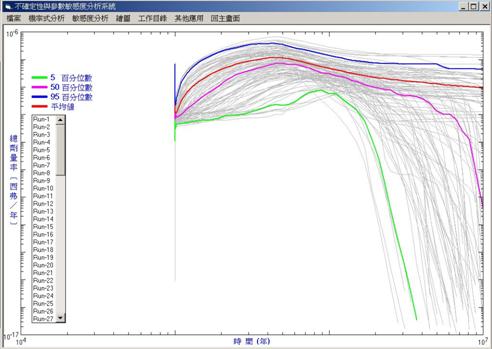
圖 6  人體總輻射劑量率隨時間變化之不確定性情形

6.2  劑量率 CCDF 分佈

圖 6中每道灰色之曲線都有一個最高點，該點就是在該評估條件下之劑量率峰值，由於圖6共有 100 道灰色曲線，因此利用圖 6 之結果可分別得到 100 個劑量率峰值，將這 100 個劑量率峰值從小到大依序排列，第 1 點之機率設為 1.0，且每個相鄰兩點間之機率差值設為 0.01，則可得到圖7所示之劑量率峰值 CCDF 圖。所謂 CCDF（即 1-CDF） 值就是數值大於等於 X 軸上之某一數值之機率：以圖7 為例，所有的劑量率峰值皆大於 2.57E-08 Sv/yr、且皆小於 4.62E-07 Sv/yr，數值為 4.49E-08 Sv/yr 時，其 CCDF值約為 0.8；數值為 7.38E-08 Sv/yr 時，其 CCDF值約為 0.5；數值為 2.04E-07 Sv/yr時，其 CCDF值約為 0.2。

 

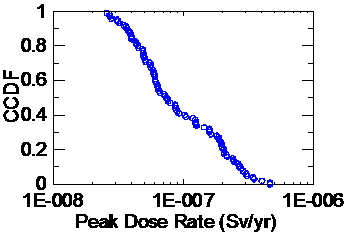
圖 7  劑量率峰值之 CCDF 機率分佈

圖 8 所示者為所有 15 道 CCDF 分佈情形，其中藍色線條為 70 個取樣點者，紅色線條為 100 個取樣點者，而黑色線條則為 200 個取樣點者。圖中之結果顯示：三種不同取樣數目下之 CCDF 分佈都非常的接近，不同取樣數目間之 CCDF 分佈差異，並不會大於相同取樣數目間之 CCDF 分佈差異。

 

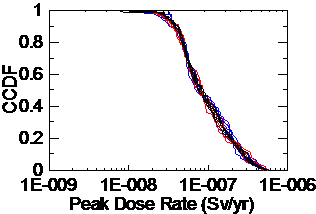
圖 8  所有 15 個情況下之 CCDF 分佈

6.3 KS-Test 結果

利用 KS-Test 技術對圖 8 中之 15 道 CCDF 分佈曲線進行交互比較分析，所得結果如圖 9 所示。圖中黑色曲線為 Kolmogorov 分佈，係根據式(2) 計算而得，藍色圓圈點為 70 個取樣點對70 個取樣點之 KS-Test 測試結果，紅色圓圈點為 100 個取樣點對100 個取樣點之 KS-Test 測試結果，餘者類推，如圖 9 上之說明。圖上亦以紫色虛線標出 a=0.05 之位置。圖中紫色垂直虛線與 X-軸之交點（即 S_m,nD_α=0.05）之數值為 1.3581。圖上之結果顯示所有不同情況之 S_m,nD 值皆小於 S_m,nD_α=0.05，因此根據 Kolmogorov 之理論，吾人可以有信心地說：對於上述之 70、100、及 200 等三種不同運跑回合數而言，他們的人體總劑量率峰值之 CCDF 分佈是相同的。

 

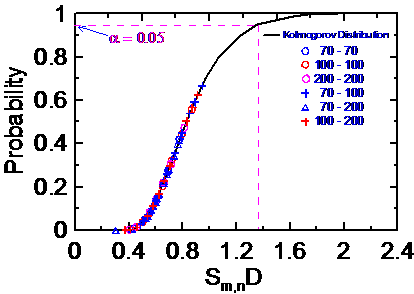
圖 9  KS-Test 結果

七、結論

本文以一用過核子燃料之深層地質處置場為研究範例，利用國際上發表之參數數據，並設定其中 67 個參數為分佈型參數，以拉丁超立體取樣技術進行機率式安全分析結果之收斂性議題探討。多重運跑回合數則分別設定為 70、100、及 200 等三種不同情況，且每種情況又各自獨立運跑五次。本文以 KS-Test 來定量地分析人體因處置場核種外釋所造成之劑量率峰值CCDF 分佈結果，KS-Test 測試結果顯示：對於本文之研究範例而言，運跑回合數 70 即可得到穩定、可靠、收斂的機率式評估結果。以美國 WIPP（Waste Isolation Pilot Plant）TRU 處置場之功能／安全評估^[27]為例，該評估具有 46 個分佈型參數，但也只運跑 60 回合而已。運跑回合數牽涉到安全分析所花之費用，能夠儘量減少運跑回合數就可減少在功能安全分析方面所花費的成本。另一方面，運跑回合數減少也可縮短電腦運跑所需之時間，降低電腦因不耐過長時間運跑而當機所造成之安全分析失敗的風險。

參考文獻

1.    SKI, “Site-94: Deep Repository Performance Assessment Project”, Vol.1 & 2, SKI Report SKI 96:36, Swedish Nuclear Power Inspectorate, Stockholm, Dec. 1996.

2.    US DOE, “Title 40 CFR Part 191 Compliance Certification Application for the Waste Isolation Pilot Plant, DOE/CAO-1996-2184”, Vols. I-XXI. Carlsbad, NM: US Department of Energy, Carlsbad Area Office, 1996.

3.    Timo Vieno and Henrik Nordman, “Safety Assessment of Spent Fuel Disposal in Hastholmen, Kivetty, Olkiluoto and Romuvaara”, TILA-99, POSIVA 99-07, OSIVA OY, Finland, March 1999.

4.    CRWMS M&O, US DOE, “Yucca Mountain Project: Total System Performance Assessment for the Site Recommendation”, TDR-WIS-PA-000001 Rev00 ICN01, Dec., 2000.

5.    JNC,〝H12: Project to Establish the Scientific and Technical Basis for HLW Disposal in Japanese – Project Overview Report〞, Japanese Nuclear Cycle Development Institute, April 2000.

6.    陳衛里，〝用過核燃料直接處置〞，核研季刊，第三期， pp.3-16，民國八十一年四月。

7.    莊文壽、洪錦雄、董家寶，〝深層地質處置技術之研究〞，核研季刊，第三十七期，pp.44-54，民國八十九年十月。

8.    洪錦雄、莊文壽、劉凌振、董家寶，〝功能／安全評估研究  --  建立深層處置場初期功能評估技術(I)〞，SNFD-INER-90-151，我國用過核燃料長程處置潛在母岩特性調查與評估階段前二年計畫，行政院原子能委員會核能研究所／工業技術研究院能源與資源研究所，委託單位：台灣電力公司，民國九十年一月。

9.  朱信忠，〝深層地質處置工程障壁外釋不確定性研究〞，台電核能月刊，第 235 期，pp.23-33，民國九十一年七月。

10.  朱信忠，〝深層地質處置工程障壁外釋之參數敏感度分析〞，台電核能月刊，第 245 期，pp.64-78，民國九十二年四月。

11.  SKBF/KBS, Final Storage of Spent Nuclear Fuel-KBS-3, vol.I：General, 1983.

12.  張瑟稀、張福麟、朱信忠、賴成銑，〝INPAG-N程式簡介及其應用〞，核研季刊，第四十期， pp.95-105，民國九十年七月。

13.  朱信忠，〝近場功能評估程式 INPAG-N 視窗操作介面之設計〞，核能研究所對內報告，INER-T2750，民國九十年十月。

14.  朱信忠、張福麟、莊文壽，〝緩衝層區塊數對 INPAG-N 程式計算結果的影響〞，台電工程月刊，第 649 期，pp.61-67，民國九十一年九月。

15.  張福麟、朱信忠、莊文壽、張瑟稀，〝緩衝層區塊數對 INPAG-F 程式計算結果的影響〞，台電工程月刊，第 654 期，pp.85-94，民國九十二年二月。

16.  Timo Vieno, WELL-97 – A Stylized Well Scenario for Indicative Dose Assessment of Deep Repositories, Espoo, VTT Energy, Technical Report SPAVTT-2/97, 1997.

17.  朱信忠，〝Kolmogorov-Smirnov 統計測試法〞，台電核能月刊，第 324 期，pp.56-66，民國九十八年十二月。

18.  ICRP, ICRP Publication 72: Age-dependent Doses to Members of the Public from Intake of Radionuclides, Part 5, Compilation of Ingestion and Inhalation Coefficients, Vol. 26/1, 1996.

19.  朱信忠，"FORTRAN-77 拉丁超立體取樣(LHS)電腦程式與放射性廢料最終處置功能評估程式參數之製備"， 核能研究所對內報告，INER-T2075，民國八十四年三月。

20.  朱信忠，"參數取樣分析技術應用於生物圈核種傳輸模式之探討"，核研季刊，第十六期，pp.51-59，民國八十四年七月。

21.  朱信忠、魏佩玉，〝參數敏感度與不確定度分析研究(I) – 拉丁超立體取樣之技術與電腦程式〞， SNFD-INER-90-093，我國用過核燃料長程處置第三階段區域調查前四年工作計畫第三工作年度計畫，行政院原子能委員會核能研究所，委託單位：台灣電力公司，民國八十六年六月。

22. 朱信忠，〝放射性廢料深層地質處置全系統功能評估 – 參數取樣系統之設計〞，核能研究所對內報告，INER-T2798，民國九十一年四月。

23.  朱信忠、吳典諺，〝系統評估及整合技術建立〞，SNFD-INER-90-505，我國用過核燃料長程處置潛在母岩特性調查與評估階段發展初步功能/安全評估模式(第一年度計畫)，行政院原子能委員會核能研究所，委託單位：台灣電力公司，民國九十一年六月。

24.  朱信忠，2008.03，參數取樣方法對機率式評估結果之影響，台電核能月刊，vol.303，pp.22-30。

25.  朱信忠，2007.07.，截端常態分佈函數之取樣技術，台電工程月刊，INER-4707，Vol.707，pp.111-114。

26.  Ju, Shin-Jon, On the Distribution Type of Uncertain Inputs for Probabilistic Assessment, Reliability Engineering and System Safety, 94(5), pp.964-968, 2009.

27.  WIPP Performance Assessment Division, “Preliminary Comparison with 40 CFR Part 191, Subpart B for the Waste Isolation Pilot Plant, December 1991, Vol.4: Uncertainty and Sensitivity Analysis Results”, SAND91-0893/4, Albuquerque, NM, Sandia National Laboratories, Dec. 1991.

< 上一則

下一則 >